트리

트리 (Tree)

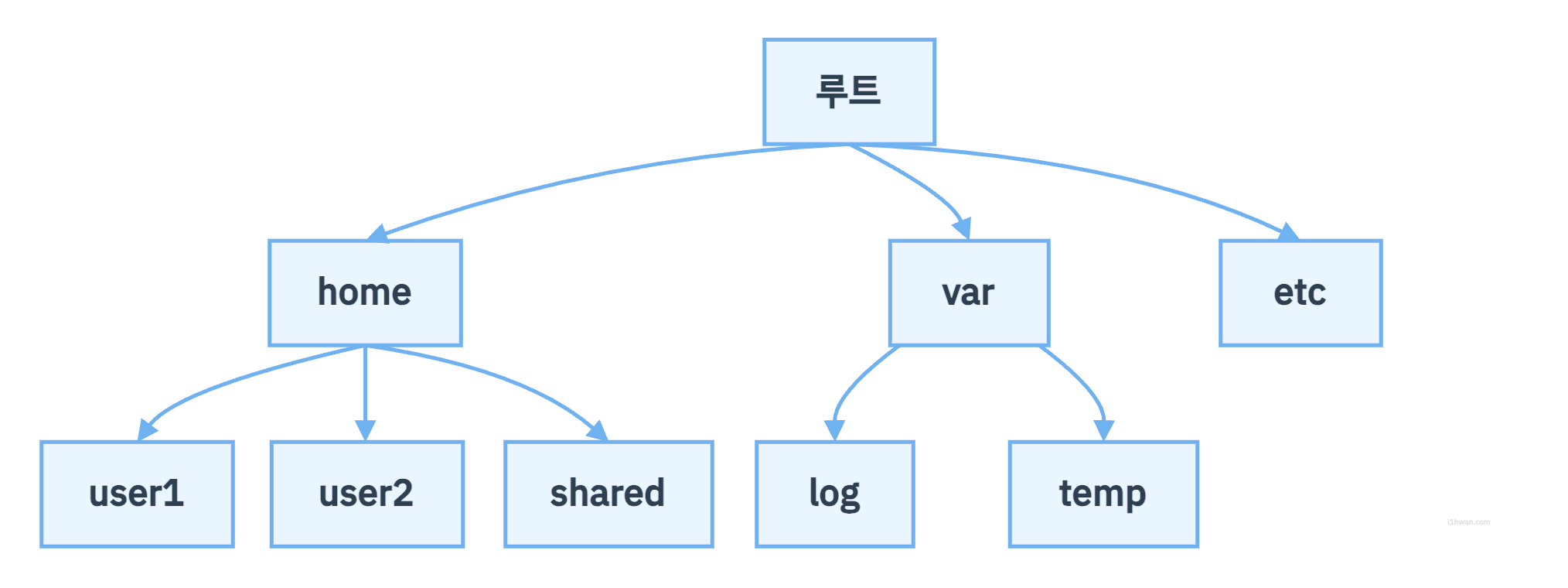
• 나무를 닮은 자료구조로, 상위 원소에서 하위 원소로 내려가면서 확장되는 나무 모양의 구조
• 원소들 간에 계층적인 관계를 나타내는 계층형 자료구조
• 원소들 간에 1:N 관계를 가지는 비선형 자료구조
• 트리는 부모-자식 관계의 노드들로 이루어짐
• 응용 분야: 가계도, 조직도, 컴퓨터의 폴더 구조, 탐색 트리, 힙 트리, 결정 트리 등

트리의 용어

• 노드 (node): 트리의 구성요소
• 간선 (edge): 노드를 연결하는 선, 즉 부모 노드와 자식 노드를 연결하는 선
• 루트 (root): 부모가 없는 노드, 트리 구조의 시작점
• 단말 노드 (terminal node 또는 leaf node): 자식이 없는 노드
• 비단말 노드 (nonterminal node 또는 internal node): 자식을 가지는 노드
• 자식, 부모, 형제, 조상, 자손 노드: 인간의 가족 관계와 유사
  • 조상 노드 (ancestor node): 간선을 따라 루트 노드까지 경로에 있는 모든 노드
  • 자손 노드 (descendant node): 특정 노드의 서브 트리에 있는 하위 레벨의 노드들
  • 형제 노드 (sibling node): 같은 부모 노드의 자식 노드들
• 차수 (degree): 노드의 자식 노드 수
  • 노드의 차수: 해당 노드에 연결된 자식 노드의 수
  • 트리의 차수: 트리에 있는 노드의 차수 중에서 가장 큰 값
• 레벨 (level): 트리의 각 층의 번호
• 높이 (height) 또는 깊이 (depth): 트리의 최대 레벨
  • 노드의 높이: 루트에서 특정 노드에 이르는 간선의 수
  • 트리의 높이: 트리에 있는 노드의 높이 중에서 가장 큰 값

서브 트리 (subtree): 하나의 노드와 그 자손들로 이루어진 트리

용어 예시

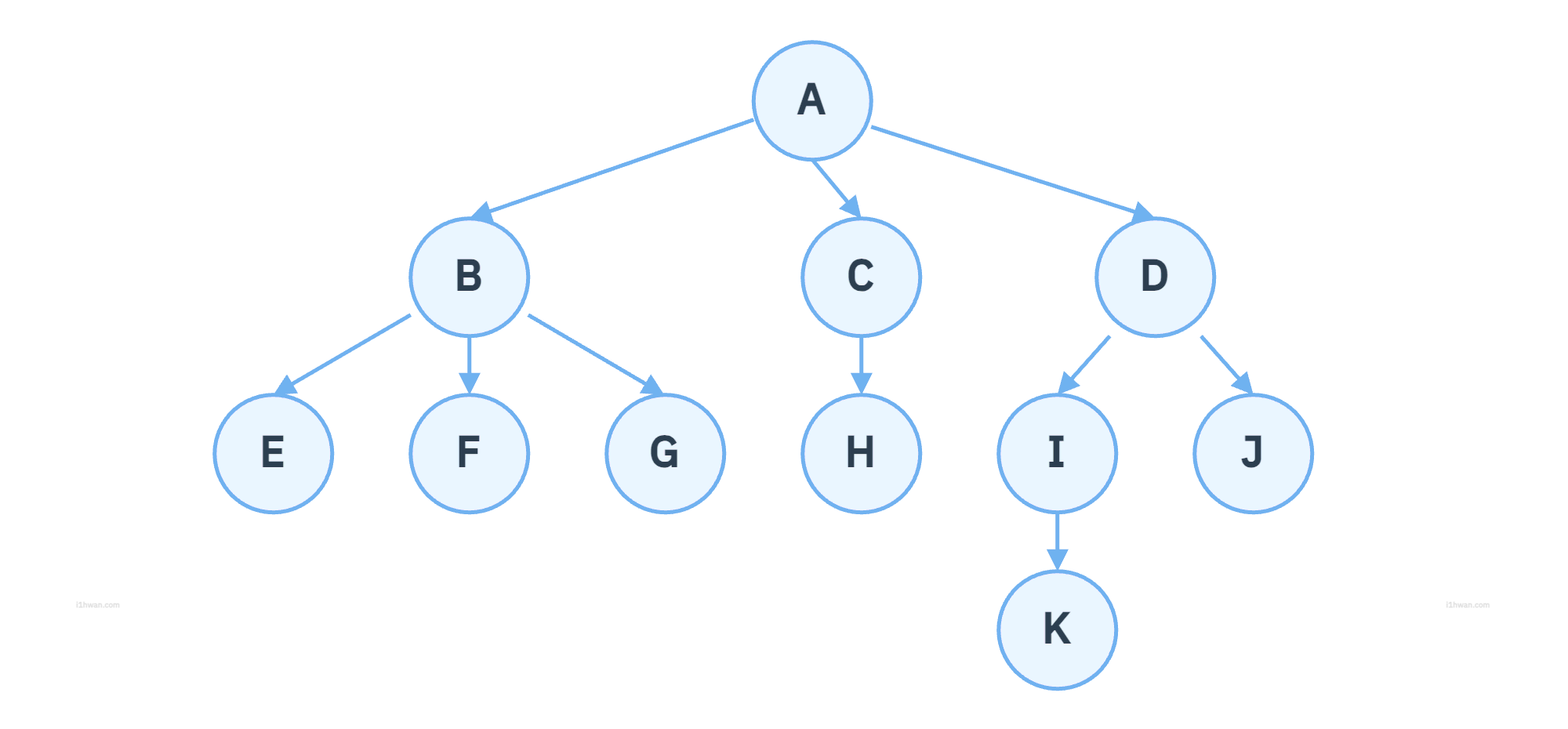
• 루트 노드: A
• C의 부모 노드: A
• D의 자식 노드: I, J
• D의 자손 노드: I, J, K
• K의 조상 노드: I, D, A
• B의 형제 노드: C, D
• D의 차수: 2 (I, J)
• 단말 노드: E, F, G, K, H, J (자식이 없는 노드들)
• 비단말 노드: A, B, C, D, I (자식이 있는 노드들)
• 트리의 높이: 4 (레벨 4까지 존재)
• 트리의 차수: 3 (A 또는 B의 차수가 3으로 가장 큼)
• 숲 (forest): 서브 트리의 집합
  • 트리에서 루트 노드(예: A)를 제거하면, A의 자식 노드들(B, C, D)을 각각 루트로 하는 여러 개의 서브 트리(트리1, 트리2, 트리3)가 생기는데, 이들의 집합을 숲이라고 함

트리의 표현 방법들

• N-링크 표현: 각 노드가 자식의 수(N)만큼 링크 필드를 가지는 방식
  • 문제점: 각 노드마다 자식의 수가 다를 수 있어, 최대 자식 수만큼 링크 공간을 할당하면 메모리 낭비가 심하거나, 특정 수로 제한하면 더 많은 자식을 표현할 수 없음
• 중첩된 집합 표현: 집합 기호를 사용하여 트리의 계층 구조를 표현
  • ex) A { B { E, F, G {K} }, C {H}, D {I, J} }
• 중첩된 괄호 표현: 괄호를 사용하여 트리의 계층 구조를 표현
  • ex) (A (B (E) (F) (G (K))) (C (H)) (D (I) (J)))
• 들여쓰기 표현: 들여쓰기를 통해 부모-자식 관계를 시각적으로 표현

이진 트리 (Binary Tree)

• 모든 노드가 2개 이하의 서브 트리를 가지고 있는 트리
• 이진 트리의 특징
  • 각 노드에는 최대 2개까지의 자식 노드가 존재
  • 이진 트리의 모든 노드는 왼쪽 자식 노드와 오른쪽 자식 노드만 가짐
  • 공백 노드도 자식 노드로 취급 (자식이 없는 경우)
  • 모든 노드의 차수가 2 이하가 되므로 구현하기가 편리함
  • 서브 트리 간에 순서가 존재 (왼쪽 서브 트리, 오른쪽 서브 트리)

이진 트리의 종류

• 포화 이진 트리
  • 모든 레벨의 노드가 포화 상태로 꽉 차있는 이진 트리
  • 높이가 $h$일 때 최대 $2^h - 1$개의 노드를 가짐
  • 루트를 1번으로 하여 $2^h - 1$까지 정해진 위치에 대한 노드 번호를 가짐 (배열 표현에 용이)
• 완전 이진 트리
  • 높이가 $h$일 때 레벨 1부터 $h - 1$까지는 노드가 모두 채워져 있음
  • 마지막 레벨 $h$에서는 노드가 왼쪽부터 순서대로 채워짐
  • 마지막 레벨 $h$에서 노드가 꽉 차지 않아도 되지만, 중간에 빈 곳이 있으면 안됨
• ex) 힙(Heap) 트리
• 균형 이진 트리
  • 모든 노드의 왼쪽 서브트리 높이와 오른쪽 서브트리 높이의 차이가 1 이하인 이진 트리
  • 탐색 연산의 효율성을 높이기 위해 사용
• 편향 이진 트리
  • 높이가 $h$일 때 $h$개의 노드를 가지면서, 모든 노드가 왼쪽이나 오른쪽 중 한 방향으로만 서브 트리를 가지고 있는 이진 트리
• 성능 면에서 연결 리스트와 유사해짐

이진 트리의 성질

• 노드의 개수가 $n$개이면 간선의 개수는 $n-1$개
  • 루트를 제외한 (n-1)개의 노드가 각각 부모 노드와 연결되는 한 개의 간선을 가짐
• 높이가 $h$인 이진 트리가 가질 수 있는 노드의 개수는 최소 $h$개 ~ 최대 $2^h - 1$개
• $n$개 노드의 이진 트리의 높이는 최소 $\log_2{(n+1)}$ ~ 최대 $n$

이진 트리의 추상 자료형

• 데이터: 노드의 집합. 공집합이거나, 루트 노드와 왼쪽 서브 트리, 오른쪽 서브 트리로 구성됨. 모든 서브 트리도 이진 트리이어야 함.
• 연산
  • init(): 이진 트리를 초기화
  • is_empty(): 이진 트리가 공백 상태인지 확인
  • create_tree(e, left, right): 이진 트리 left와 right를 받아 e를 루트로 하는 이진 트리를 생성
  • get_root(): 이진 트리의 루트 노드를 반환
  • get_count(): 이진 트리의 노드 수를 반환
  • get_leaf_count(): 이진 트리의 단말 노드의 수를 반환
  • get_height(): 이진 트리의 높이를 반환

이진 트리의 구현

배열 표현법

• 모든 이진 트리를 포화 이진 트리라고 가정하고 배열에 저장
• 각 노드에 번호를 붙여서 그 번호를 배열의 인덱스로 삼아 노드의 데이터를 배열에 저장
  • 루트는 인덱스 1
  • 노드 인덱스 i의 왼쪽 자식 인덱스: 2*i
  • 노드 인덱스 i의 오른쪽 자식 인덱스: 2*i + 1
  • 노드 인덱스 i의 부모 인덱스: i/2
• 장점: 노드 간 관계를 인덱스 계산으로 쉽게 알 수 있음. 완전 이진 트리의 경우 메모리 낭비가 적음.
• 단점: 편향 이진 트리나 희소한 트리의 경우 사용하지 않는 배열 공간이 많아져 메모리 낭비가 심함. 트리의 크기가 커지면 배열 크기도 매우 커져야 함.

링크 표현법

• 부모 노드가 자식 노드를 가리키게 하는 방법
• 노드와 포인터를 이용
• 각 노드는 데이터 필드와 왼쪽 자식, 오른쪽 자식을 가리키는 두 개의 포인터 필드로 구성

이진 트리의 순회 (Traversal)

• 순회 (traversal): 트리의 모든 노드들을 체계적으로 한 번씩 방문하는 작업
• 선형 자료구조의 순회: 보통 하나의 방법만 존재 (처음부터 끝까지)
• 이진 트리의 순회: 비선형 자료구조이므로 다양한 순회 방법이 존재

이진 트리의 기본 순회

• V: 현재 노드(Vertex/Root) 방문
• L: 왼쪽 서브트리(Left Subtree) 순회
• R: 오른쪽 서브트리(Right Subtree) 순회

전위 순회: VLR

• 루트(V) → 왼쪽 자식(L) → 오른쪽 자식(R) 순서로 방문
  ex) 문서의 목차를 출력할 때 (큰 제목 -> 작은 제목 순)

preorder(node n)
    if n != NULL:
        VisitNode(n)      // 루트 n이 NULL이 아닐 때만 처리, 루트 노드 처리
        preorder(n.left)  // 왼쪽 서브 트리 처리
        preorder(n.right) // 오른쪽 서브 트리 처리

// 가계도 노드
typedef struct FamilyMember {
    char name[50];
    struct FamilyMember* first_child;  // 왼쪽 자식 역할
    struct FamilyMember* second_child; // 오른쪽 자식 역할
} FamilyMember;

void visit_member_name(FamilyMember* member) {
    if (member) printf("%s ", member->name);
}

// 전위 순회: 조상부터 자손 순으로 가족 구성원 이름 출력
// 예: "할아버지 아빠 첫째손자 둘째손자 (고모/이모)..."
void preorder_family_visit(FamilyMember* member) {
    if (member == NULL) return;
    visit_member_name(member);                  // 현재 가족 구성원 방문 (V) (ex: '할아버지' 이름 출력)
    preorder_family_visit(member->first_child);  // 첫째 자식 라인 방문 (L) (ex: '아빠'와 그 자손들 방문)
    preorder_family_visit(member->second_child); // 둘째 자식 라인 방문 (R) (ex: '고모/이모'와 그 자손들 방문)
}

중위 순회: LVR

• 왼쪽 자식(L) → 루트(V) → 오른쪽 자식(R) 순서로 방문
  ex) 이진 탐색 트리에서 노드를 정렬된 순서로 방문할 때 사용

inorder(node n)
    if n != NULL:
        inorder(n.left)   // 왼쪽 서브 트리 처리
        VisitNode(n)      // 루트 노드 처리
        inorder(n.right)  // 오른쪽 서브 트리 처리

// 중위 순회: 주로 정렬된 순서로 데이터 처리 시 사용 (BST의 경우)
// 예: 가계도에서 왼쪽 자손부터 시작해 부모를 거쳐 오른쪽 자손으로 방문
void inorder_family_visit(FamilyMember* member) {
    if (member == NULL) return;
    inorder_family_visit(member->first_child);  // 첫째 자식 라인 방문 (L) (ex: '첫째손자'부터 방문)
    visit_member_name(member);                  // 현재 가족 구성원 방문 (V) (ex: '아빠' 이름 출력)
    inorder_family_visit(member->second_child); // 둘째 자식 라인 방문 (R) (ex: '둘째손자' 방문)
}

후위 순회: LRV

• 왼쪽 자식(L) → 오른쪽 자식(R) → 루트(V) 순서로 방문
  ex) 폴더 용량 계산 (하위 폴더/파일 크기를 모두 더한 후 현재 폴더 크기 계산), 트리 삭제

postorder(node n)
    if n != NULL:
        postorder(n.left)  // 왼쪽 서브 트리 처리
        postorder(n.right) // 오른쪽 서브 트리 처리
        VisitNode(n)       // 루트 노드 처리

// 후위 순회: 자식 노드들을 먼저 처리하고 부모 노드를 처리할 때 사용
// 예: 가계도에서 가장 말단 자손부터 시작해 부모로 거슬러 올라가며 방문
void postorder_family_visit(FamilyMember* member) {
    if (member == NULL) return;
    postorder_family_visit(member->first_child);  // 첫째 자식 라인 방문 (L) (ex: '첫째손자'부터 방문)
    postorder_family_visit(member->second_child); // 둘째 자식 라인 방문 (R) (ex: '둘째손자' 방문)
    visit_member_name(member);                  // 현재 가족 구성원 방문 (V) (ex: '아빠' 이름 마지막에 출력)
}

레벨 순회 (Level Order Traversal)

• 노드를 레벨 순으로 검사하는 순회방법 (낮은 레벨부터, 같은 레벨에서는 왼쪽에서 오른쪽으로)

levelorder(root)
    if root != NULL:
        init_queue()
        enqueue(root)
        while not is_empty(queue):
            n = dequeue()
            if n != NULL:
                VisitNode(n)
                enqueue(n.left)
                enqueue(n.right)

순회 방법에 따른 노드 방문 순서

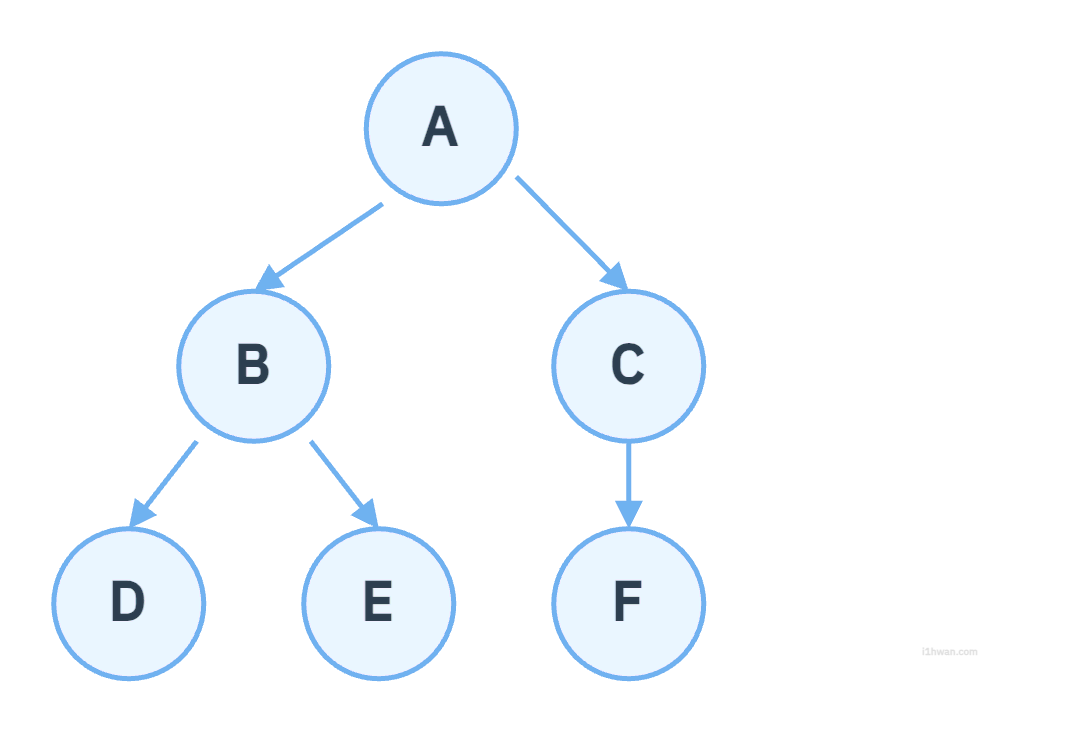
• 전위순회 (VLR): A → B → D → E → C → F
• 중위순회 (LVR): D → B → E → A → C → F
• 후위순회 (LRV): D → E → B → F → C → A
• 레벨순회 (Level): A → B → C → D → E → F

이진 트리의 추가 연산

트리의 노드 개수 구하기

• 재귀적 정의: N_total = N_left + N_right + 1 (왼쪽 서브트리 노드 수 + 오른쪽 서브트리 노드 수 + 루트 노드 1개)

count_node(n)
    if n = NULL: return 0
    n_left = count_node(n.left)    // 왼쪽 서브 트리 처리
    n_right = count_node(n.right)  // 오른쪽 서브 트리 처리
    return 1 + n_left + n_right    // 루트 노드 처리

// 웹사이트의 총 페이지 수 계산
typedef struct WebPageNode {
    char url[256];
    struct WebPageNode* sub_page1; // 왼쪽 자식
    struct WebPageNode* sub_page2; // 오른쪽 자식
} WebPageNode;

int count_total_web_pages(WebPageNode* page) {
    if (page == NULL) {
        return 0; // 빈 페이지(서브트리)는 0개
    }
    // 현재 페이지(1) + 첫 번째 하위 페이지들의 수 + 두 번째 하위 페이지들의 수
    return 1 + count_total_web_pages(page->sub_page1) + count_total_web_pages(page->sub_page2);
}

트리의 높이 구하기

• 서브 트리들의 높이 중에서 최대값을 구하여 1을 더한 값을 반환
• 재귀적 정의: height = max(h_left, h_right) + 1

calc_height(n)
    if n = NULL: return 0 // 또는 -1 (간선 기준)
    else: return 1 + max(calc_height(n.left), calc_height(n.right))

// 프로젝트에서 가장 깊은 작업 단계 계산
// (TaskNode 구조체 재활용)
int calculate_project_depth(TaskNode* task) {
    if (task == NULL) {
        return -1; // 빈 작업(서브트리)의 높이는 -1 (또는 0, 정의에 따라 다름. 여기선 간선 수 기준이므로 -1)
                   // 노드 수 기준이면 0
    }
    int left_depth = calculate_project_depth(task->sub_task1);
    int right_depth = calculate_project_depth(task->sub_task2);

    return (left_depth > right_depth ? left_depth : right_depth) + 1;
}

노드의 레벨 구하기

• 전위순회 방식으로 트리를 탐색하면서 현재 레벨을 전달, key를 찾으면 해당 레벨 반환

calc_level(n, key, level)
    if n = NULL: return 0 // 레벨이 결정되지 않음 (0 또는 음수)
    if n.key = key: return level // 레벨이 결정됨 (> 0)
    
    lev = calc_level(n.left, key, level+1) // 왼쪽 서브 트리 처리
    if lev > 0: return lev // 왼쪽에서 찾았으면 반환
    else: return calc_level(n.right, key, level+1) // 오른쪽 서브 트리 처리

// 조직도에서 특정 직원의 직급 레벨(CEO=1) 찾기
// (EmployeeNode 구조체 재활용)
int find_employee_level(EmployeeNode* current_employee, const char* target_name, int current_level) {
    if (current_employee == NULL) {
        return 0; // 찾지 못함 (또는 -1)
    }
    if (strcmp(current_employee->name, target_name) == 0) {
        return current_level; // 찾음! 현재 레벨 반환
    }

    // 왼쪽(첫 번째 부하) 서브트리에서 찾기
    int found_level = find_employee_level(current_employee->direct_report1, target_name, current_level + 1);
    if (found_level > 0) { // 왼쪽에서 찾았으면 반환
        return found_level;
    }

    // 오른쪽(두 번째 부하) 서브트리에서 찾기
    found_level = find_employee_level(current_employee->direct_report2, target_name, current_level + 1);
    return found_level; // 오른쪽에서 찾았거나 못 찾았으면 그 결과 반환
}

단말 노드의 개수 구하기

• 트리의 단말노드(자식이 없는 노드) 개수를 계산

count_leaf(x)
    if x = NULL then return 0;
    if x.left=NULL and x.right=NULL // 현재 노드가 단말 노드이면
        then return 1;
    else return count_leaf(x.left) + count_leaf(x.right); // 단말이 아니면 자식들의 단말 수 합

// 의사결정 트리에서 최종 결정(잎 노드)의 가짓수 계산
typedef struct DecisionNode {
    char criteria[100]; // 결정 기준 또는 최종 결정
    struct DecisionNode* yes_branch; // 왼쪽 자식
    struct DecisionNode* no_branch;  // 오른쪽 자식
} DecisionNode;

int count_final_decisions(DecisionNode* node) {
    if (node == NULL) {
        return 0;
    }
    // 자식이 없으면 단말 노드 (최종 결정)
    if (node->yes_branch == NULL && node->no_branch == NULL) {
        return 1;
    }
    // 자식이 있으면, 왼쪽과 오른쪽 서브트리의 단말 노드 수 합산
    return count_final_decisions(node->yes_branch) + count_final_decisions(node->no_branch);
}

트리를 좌우로 대칭시키기

• 트리의 각 노드에서 왼쪽 자식과 오른쪽 자식을 서로 바꿈

reverse(n) // 또는 mirror(n)
    if n != NULL :
        // 루트 처리: 좌우 서브 트리를 교환
        temp = n.left
        n.left = n.right
        n.right = temp
        
        reverse(n.left)  // (새로운) 왼쪽 서브 트리 처리
        reverse(n.right) // (새로운) 오른쪽 서브 트리 처리

// 메뉴 항목의 표시 순서를 좌우 반전
typedef struct MenuItemNode {
    char item_name[50];
    struct MenuItemNode* left_submenu;  // 원래 왼쪽 서브메뉴
    struct MenuItemNode* right_submenu; // 원래 오른쪽 서브메뉴
} MenuItemNode;

void invert_menu_order(MenuItemNode* item) {
    if (item == NULL) {
        return;
    }

    // 현재 노드의 좌우 자식(서브메뉴) 교환
    MenuItemNode* temp = item->left_submenu;
    item->left_submenu = item->right_submenu;
    item->right_submenu = temp;

    // 각 자식(서브메뉴)에 대해 재귀적으로 반전 수행
    invert_menu_order(item->left_submenu);  // 새로 왼쪽이 된 서브메뉴 (원래 오른쪽)에 대해 반전
    invert_menu_order(item->right_submenu); // 새로 오른쪽이 된 서브메뉴 (원래 왼쪽)에 대해 반전
}

수식 트리 (Expression Tree)

• 산술식을 트리 형태로 표현한 것
  • 비단말노드: 연산자(operator)
  • 단말노드: 피연산자(operand)

수식 트리 계산

• 후위순회를 사용 (LRV: 왼쪽 계산, 오른쪽 계산, 연산 수행)
• 서브트리의 값을 순환호출(재귀)로 계산
• 비단말노드(연산자)는 양쪽 서브트리(피연산자)의 값을 해당 연산자로 계산

evaluate(exp) // exp는 수식 트리의 노드를 가리키는 포인터
    if exp = NULL then return 0; // 또는 오류
    else if exp is an operand then return value(exp); // 단말 노드(피연산자)면 값 반환
    else // 연산자 노드이면
        x <- evaluate(LEFT(exp));  // 왼쪽 서브트리 계산
        y <- evaluate(RIGHT(exp)); // 오른쪽 서브트리 계산
        op <- DATA(exp);          // 현재 노드의 연산자
        return (x op y);          // 계산 결과 반환

// 수식 트리 노드 구조체
typedef struct ExprNode {
    int is_operand; // 0이면 연산자, 1이면 피연산자
    union {
        char operator_char; // 연산자 (+, -, *, /)
        int operand_value;  // 피연산자 (숫자)
    } data;
    struct ExprNode* left;
    struct ExprNode* right;
} ExprNode;

int evaluate_expression_tree(ExprNode* node) {
    if (node == NULL) {
        fprintf(stderr, "Error: Null node in expression tree.\n");
        return 0; 
    }

    if (node->is_operand) { // 단말 노드 (피연산자)
        return node->data.operand_value;
    } else { // 비단말 노드 (연산자)
        int left_val = evaluate_expression_tree(node->left);
        int right_val = evaluate_expression_tree(node->right);
        char operator = node->data.operator_char;

        printf("Calculating: %d %c %d\n", left_val, operator, right_val); // 계산 과정 시각화

        switch (operator) {
            case '+': return left_val + right_val;
            case '-': return left_val - right_val;
            case '*': return left_val * right_val;
            case '/': 
                if (right_val == 0) {
                    fprintf(stderr, "Error: Division by zero.\n");
                    return 0;
                }
                return left_val / right_val;
            default:
                fprintf(stderr, "Error: Unknown operator %c.\n", operator);
                return 0;
        }
    }
}

이진 탐색 트리 (BST)

• 탐색(search): 가장 중요한 컴퓨터 응용 중 하나로, 레코드의 집합에서 특정한 레코드를 찾아내는 연산
• 이진 탐색 트리 (BST: Binary Search Tree): 효율적인 탐색을 위한 이진 트리 기반의 자료구조
• 이진 탐색 트리의 정의
  1. 모든 노드는 유일한 키(key)를 갖는다.
  2. 임의의 노드에서, 왼쪽 서브 트리의 모든 키는 루트(현재 노드)의 키보다 작다.
  3. 임의의 노드에서, 오른쪽 서브 트리의 모든 키는 루트(현재 노드)의 키보다 크다.
  4. 왼쪽과 오른쪽 서브 트리도 모두 이진 탐색 트리이다.
• 이진 탐색 트리를 중위 순회(LVR)하면 키 값들이 오름차순으로 정렬된 순서로 값을 얻을 수 있다.

탐색 관련 용어

• 레코드 (record): 관련된 필드들의 모임 (ex:한 학생의 정보)
• 필드 (field): 레코드를 구성하는 각 항목 (ex: 학번, 이름, 주소)
• 테이블 (table): 레코드들의 집합 (ex: 학생 정보 전체 목록)
• 키 (key): 레코드를 유일하게 식별하거나 검색 기준으로 사용되는 필드 (ex: 학번)
• 주요 키 (primary key): 레코드를 유일하게 식별하는 키 (중복 허용 안됨)

이진 탐색 트리의 탐색 연산

• 루트에서 시작
• 탐색할 키 값 x를 현재 노드의 키 값과 비교
  • x == 현재 노드의 키 값: 원하는 원소 발견, 탐색 성공
  • x < 현재 노드의 키 값: 현재 노드의 왼쪽 서브 트리에 대해 다시 탐색 연산 수행
  • x > 현재 노드의 키 값: 현재 노드의 오른쪽 서브 트리에 대해 다시 탐색 연산 수행
• 서브 트리에 대해서 순환적으로(재귀적으로) 탐색 연산을 반복

// 도서관에서 ISBN으로 책을 찾는 예시
typedef struct BookNode {
    long isbn; // 책의 고유 식별 번호 (키)
    char title[100];
    char author[50];
    struct BookNode* left_by_isbn;  // ISBN이 더 작은 책들
    struct BookNode* right_by_isbn; // ISBN이 더 큰 책들
} BookNode;

BookNode* find_book_recursive(BookNode* current_book, long target_isbn) {
    if (current_book == NULL) { // 책장에 더 이상 책이 없거나, 해당 위치에 책이 없음
        return NULL; // 탐색 실패
    }

    if (target_isbn == current_book->isbn) { // 찾았다!
        return current_book; // 탐색 성공, 해당 책 노드 반환
    } else if (target_isbn < current_book->isbn) { // 찾으려는 ISBN이 현재 책 ISBN보다 작으면
        return find_book_recursive(current_book->left_by_isbn, target_isbn); // 왼쪽 서가(서브트리)에서 계속 찾기
    } else { // 찾으려는 ISBN이 현재 책 ISBN보다 크면
        return find_book_recursive(current_book->right_by_isbn, target_isbn); // 오른쪽 서가(서브트리)에서 계속 찾기
    }
}

이진 탐색 트리의 삽입 연산

• 먼저 탐색 연산을 수행
  • 삽입할 원소와 같은 원소가 트리에 있으면 삽입할 수 없으므로 (키 중복 불가), 같은 원소가 트리에 있는지 탐색하여 확인
  • 탐색에서 탐색 실패가 결정되는 위치가 삽입 위치가 됨 (즉, NULL 포인터를 만나는 지점)
• 탐색 실패한 위치에 새로운 노드(원소)를 삽입

// 새 책 정보를 ISBN 기준으로 BST에 추가
BookNode* insert_book_recursive(BookNode* current_book_node, long new_isbn, const char* new_title, const char* new_author) {
    // 1. 삽입 위치 탐색 (재귀적으로 내려감)
    if (current_book_node == NULL) { // 여기가 삽입 위치 (탐색 실패 지점)
        BookNode* new_book = (BookNode*)malloc(sizeof(BookNode));
        if (!new_book) return NULL; // 메모리 할당 실패
        new_book->isbn = new_isbn;
        strcpy(new_book->title, new_title);
        strcpy(new_book->author, new_author);
        new_book->left_by_isbn = NULL;
        new_book->right_by_isbn = NULL;
        return new_book; // 새로 삽입된 노드가 이 서브트리의 루트가 됨
    }

    // 2. 중복 키 확인 및 다음 탐색 위치 결정
    if (new_isbn < current_book_node->isbn) {
        current_book_node->left_by_isbn = insert_book_recursive(current_book_node->left_by_isbn, new_isbn, new_title, new_author);
    } else if (new_isbn > current_book_node->isbn) {
        current_book_node->right_by_isbn = insert_book_recursive(current_book_node->right_by_isbn, new_isbn, new_title, new_author);
    } else {
        // new_isbn == current_book_node->isbn: 중복된 키, 삽입하지 않음 (또는 업데이트 로직 추가 가능)
        printf("ISBN %ld already exists. Insertion failed.\n", new_isbn);
    }
    return current_book_node; // 현재 노드 반환 (트리 구조 유지)
}

이진 탐색 트리의 삭제 연산

• 먼저 탐색 연산을 수행하여 삭제할 노드의 위치를 찾음
• 탐색하여 찾은 노드를 삭제
  • 노드의 삭제 후에도 이진 탐색 트리를 유지해야 하므로, 삭제 노드의 경우에 대한 후속 처리(이진 탐색 트리의 재구성 작업)가 필요함
• 삭제 노드의 3가지 경우
  1. CASE 1: 단말 노드인 경우 (차수 = 0)
     • 해당 노드를 단순히 삭제하고, 부모 노드의 해당 자식 링크를 NULL로 변경
  2. CASE 2: 자식 노드를 한 개 가진 경우 (차수 = 1)
     • 삭제할 노드를 제거하고, 그 자리에 삭제할 노드의 유일한 자식 노드를 연결 (부모 노드가 삭제된 노드의 자식을 직접 가리키도록 함)
  3. CASE 3: 자식 노드를 두 개 가진 경우 (차수 = 2)
     • 삭제할 노드의 자리를 대체할 후계자(successor) 노드를 선택
     • 후계자 선택 방법
       • 방법 1: 삭제할 노드의 왼쪽 서브트리에서 가장 큰 값을 가진 노드 (왼쪽 자식으로 가서 계속 오른쪽으로 이동하여 가장 오른쪽에 있는 노드)
       • 방법 2: 삭제할 노드의 오른쪽 서브트리에서 가장 작은 값을 가진 노드 (오른쪽 자식으로 가서 계속 왼쪽으로 이동하여 가장 왼쪽에 있는 노드)
     • 후계자 노드의 데이터를 삭제할 노드의 위치로 복사
     • 이제 후계자 노드가 원래 위치에서 중복되므로, 원래 위치의 후계자 노드를 삭제 (이때 후계자 노드는 차수가 0 또는 1이므로 CASE 1 또는 CASE 2에 해당)

// 오른쪽 서브트리에서 가장 작은 ISBN을 가진 책을 찾는 함수
BookNode* find_min_isbn_book(BookNode* node) {
    BookNode* current = node;
    while (current && current->left_by_isbn != NULL) { // 가장 왼쪽 노드로 이동
        current = current->left_by_isbn;
    }
    return current;
}

// 책 정보를 ISBN 기준으로 BST에서 제거
BookNode* delete_book_recursive(BookNode* root_node, long target_isbn) {
    if (root_node == NULL) return root_node; // 삭제할 책이 없음

    // 1. 삭제할 책 탐색
    if (target_isbn < root_node->isbn) {
        root_node->left_by_isbn = delete_book_recursive(root_node->left_by_isbn, target_isbn);
    } else if (target_isbn > root_node->isbn) {
        root_node->right_by_isbn = delete_book_recursive(root_node->right_by_isbn, target_isbn);
    } else { // target_isbn == root_node->isbn : 삭제할 책을 찾음!
        // CASE 1: 자식이 없거나 하나만 있는 경우
        if (root_node->left_by_isbn == NULL) {
            BookNode* temp = root_node->right_by_isbn;
            printf("Deleting book ISBN: %ld (Title: %s) - Case 1/2 (no left child)\n", root_node->isbn, root_node->title);
            free(root_node);
            return temp; // 오른쪽 자식이 새로운 루트가 되거나 NULL
        } else if (root_node->right_by_isbn == NULL) {
            BookNode* temp = root_node->left_by_isbn;
            printf("Deleting book ISBN: %ld (Title: %s) - Case 1/2 (no right child)\n", root_node->isbn, root_node->title);
            free(root_node);
            return temp; // 왼쪽 자식이 새로운 루트가 됨
        }

        // CASE 3: 자식이 둘 다 있는 경우
        // 오른쪽 서브트리에서 가장 작은 값(후계자)을 찾음
        BookNode* successor = find_min_isbn_book(root_node->right_by_isbn);
        printf("Deleting book ISBN: %ld (Title: %s) - Case 3. Successor ISBN: %ld\n", root_node->isbn, root_node->title, successor->isbn);

        // 후계자의 데이터를 현재 노드로 복사
        root_node->isbn = successor->isbn;
        strcpy(root_node->title, successor->title);
        strcpy(root_node->author, successor->author);

        // 오른쪽 서브트리에서 원래 후계자 노드를 삭제
        root_node->right_by_isbn = delete_book_recursive(root_node->right_by_isbn, successor->isbn);
    }
    return root_node; // 수정된 트리 루트 반환
}

이진 탐색 트리의 성능

• 이진 탐색 트리에서의 탐색, 삽입, 삭제 연산의 시간 복잡도는 트리의 높이 $h$에 비례: $O(h)$
• $n$개의 노드를 가지는 이진 탐색 트리의 경우
  • 최선의 경우 (Best Case): 트리가 균형적으로 생성되어 있을 때 (포화 이진 트리 또는 완전 이진 트리)
    • 높이 $h ≈ \log_2{n}$
    • 시간 복잡도: $O(\log_2{n})$
  • 최악의 경우 (Worst Case): 트리가 한쪽으로 치우쳐 생성되어 있을 때 (편향 이진 트리)
    • 높이 $h = n$
    • 시간 복잡도: $O(n)$

힙 트리 (Heap)

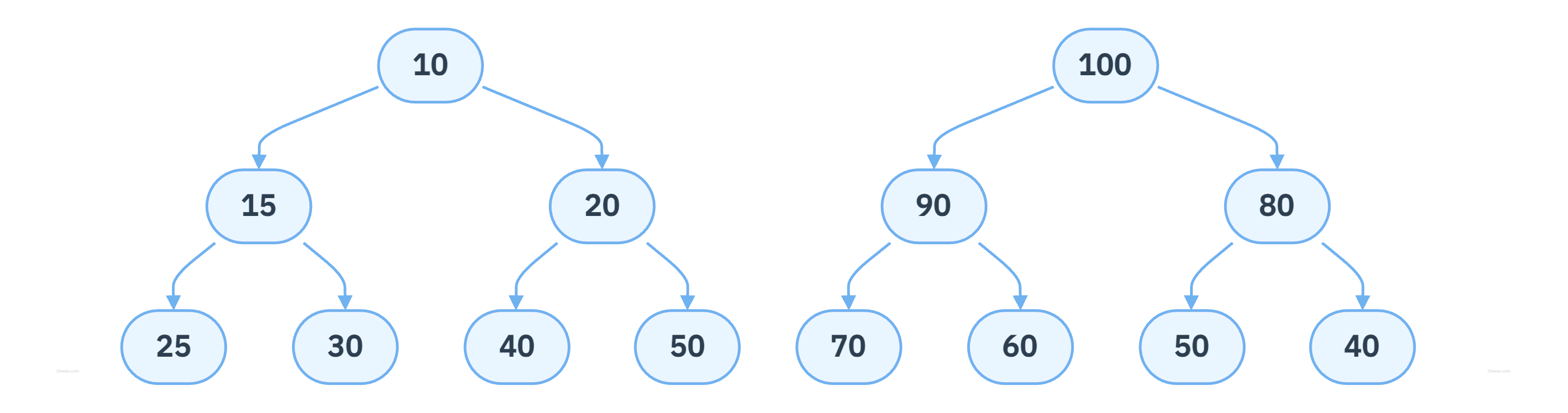
• 힙 (heap): 완전 이진 트리의 일종으로, 특별한 속성을 만족하는 트리 기반의 자료구조
• 키(key)값이 가장 큰 (또는 작은) 노드를 빨리 찾을 수 있도록 설계됨 (주로 우선순위 큐 구현에 사용)
• 최대 힙 (Max Heap)
  • 부모 노드의 키값이 자식 노드의 키값보다 크거나 같은 완전 이진 트리
  • 루트 노드는 항상 가장 큰 값을 가짐
• 최소 힙 (Min Heap)
  • 부모 노드의 키값이 자식 노드의 키값보다 작거나 같은 완전 이진 트리
  • 루트 노드는 항상 가장 작은 값을 가짐
• 힙 트리가 아닌 경우
  • 완전 이진 트리가 아닌 경우 (마지막 레벨이 왼쪽부터 채워지지 않는 경우)
  • 크기 조건을 만족하지 않는 노드가 있는 경우 (최대 힙인데 부모가 자식보다 작은 경우)

힙 트리의 표현

• 힙은 완전 이진 트리이므로 배열을 사용하여 효율적으로 표현 가능 (메모리 낭비 적음)
• 배열 인덱스 1부터 사용한다고 가정
  • k번 노드의 부모 인덱스: PARENT(k) = k / 2
  • k번 노드의 왼쪽 자식 인덱스: LEFT(k) = k * 2
  • k번 노드의 오른쪽 자식 인덱스: RIGHT(k) = k * 2 + 1

힙의 삽입 연산 (Up-heap)

• 과정 (최대 힙 기준)
  1. 새로운 노드를 힙의 마지막 위치 (완전 이진 트리를 유지하는 다음 위치)에 삽입
  2. 삽입된 노드의 키 값과 그 부모 노드의 키 값을 비교
  3. 만약 삽입된 노드의 키 값이 부모 노드의 키 값보다 크면, 두 노드의 위치를 교환
  4. 이 과정을 삽입된 노드가 올바른 위치를 찾거나 루트에 도달할 때까지 반복
• 시간 복잡도: $O(log_2{n})$

// 새로운 작업 요청을 우선순위 큐(최대 힙으로 구현)에 추가하는 예시
#define MAX_HEAP_SIZE 100
typedef struct TaskRequest {
    int priority; // 숫자가 클수록 높은 우선순위 (최대 힙)
    char description[100];
} TaskRequest;

TaskRequest task_heap[MAX_HEAP_SIZE]; // 인덱스 0은 사용 안함
int heap_count = 0; // 현재 힙에 저장된 작업 요청 수

void heap_push_task(TaskRequest new_task) {
    if (heap_count >= MAX_HEAP_SIZE - 1) {
        printf("Priority queue (heap) is full!\n");
        return;
    }
    heap_count++; // 요소 개수 증가
    int current_idx = heap_count; // 새 요소는 마지막에 삽입

    // Up-heap 과정: 부모와 비교하며 올바른 위치 찾기
    // 현재 위치가 루트가 아니고(current_idx > 1), 현재 요소의 우선순위가 부모보다 높으면
    while (current_idx > 1 && new_task.priority > task_heap[current_idx / 2].priority) {
        task_heap[current_idx] = task_heap[current_idx / 2]; // 부모 요소를 현재 위치로 내림
        current_idx /= 2; // 한 레벨 위로 이동
    }
    task_heap[current_idx] = new_task; // 찾은 위치에 새 요소 삽입
    printf("Task '%s' (Prio: %d) added. Heap: ", new_task.description, new_task.priority);
    // print_heap(); // 힙 내용 출력 함수 (생략)
}

힙의 삭제 연산 (Down-heap)

• 힙에서의 삭제는 루트 노드 삭제를 의미
• 과정 (최대 힙 기준)
  1. 루트 노드의 값을 반환하고 루트 노드를 삭제
  2. 힙의 마지막 노드를 루트 위치로 가져옴
  3. 새로운 루트 노드의 키 값과 그 자식 노드들의 키 값을 비교 (두 자식 중 더 큰 자식과 비교)
  4. 만약 루트 노드의 키 값이 더 큰 자식 노드의 키 값보다 작으면, 두 노드의 위치를 교환
  5. 이 과정을 교환된 노드가 올바른 위치를 찾거나 단말 노드에 도달할 때까지 반복
• 시간 복잡도: $O(log_2{n})$

// 우선순위 큐(최대 힙)에서 가장 긴급한 작업(루트)을 처리하고 제거하는 예시
TaskRequest heap_pop_task() {
    if (heap_count == 0) {
        printf("Priority queue (heap) is empty!\n");
        TaskRequest empty_task = {-1, "EMPTY"}; // 오류 또는 빈 값 표시
        return empty_task;
    }

    TaskRequest root_task = task_heap[1]; // 반환할 루트 작업 (가장 우선순위 높은 작업)
    TaskRequest last_task = task_heap[heap_count]; // 마지막 작업을 루트로 옮길 준비
    heap_count--; // 요소 개수 감소

    if (heap_count == 0) { // 힙이 비게 되면 바로 반환
        return root_task;
    }

    // Down-heap 과정
    int parent_idx = 1; // 현재 노드 (루트에서 시작)
    int child_idx;
    task_heap[parent_idx] = last_task; // 마지막 작업을 루트로 이동

    while (1) {
        child_idx = parent_idx * 2; // 왼쪽 자식 인덱스
        if (child_idx > heap_count) { // 자식이 없으면 종료 (단말 도달)
            break;
        }
        // 오른쪽 자식이 존재하고, 오른쪽 자식의 우선순위가 왼쪽 자식보다 높으면
        if (child_idx + 1 <= heap_count && task_heap[child_idx + 1].priority > task_heap[child_idx].priority) {
            child_idx++; // 더 큰 자식(오른쪽)을 선택
        }

        // 부모(현재 노드)의 우선순위가 선택된 자식보다 크거나 같으면 제자리 찾음, 종료
        if (task_heap[parent_idx].priority >= task_heap[child_idx].priority) {
            break;
        }

        // 부모와 자식 교환
        TaskRequest temp = task_heap[parent_idx];
        task_heap[parent_idx] = task_heap[child_idx];
        task_heap[child_idx] = temp;

        parent_idx = child_idx; // 다음 비교를 위해 한 레벨 아래로 이동
    }
    printf("Task '%s' (Prio: %d) processed. Heap: ", root_task.description, root_task.priority);
    // print_heap(); // 힙 내용 출력 함수 (생략)
    return root_task;
}

배열이 최대 힙인지 검사하기

• 배열로 표현된 트리가 최대 힙의 조건을 만족하는지 검사
• 모든 부모 노드에 대해 부모 키 >= 자식 키 조건을 확인
• 내부 노드(자식이 있는 노드)들만 검사하면 됨. 배열의 1부터 len/2 까지만 검사

// 환자 대기열(최소 힙으로 가정)이 올바르게 유지되고 있는지 검사하는 예시
// (HNode는 환자 정보, priority는 응급도 - 낮을수록 긴급)
typedef struct PatientNode {
    int patient_id;
    int priority; // 응급도 (숫자가 작을수록 긴급 - 최소 힙)
} PatientNode; // HNode 대신 사용

#define LEFT_CHILD(i) (2*(i))
#define RIGHT_CHILD(i) (2*(i) + 1)

// 배열 arr이 최소 힙인지 검사 (인덱스 1부터 시작, len은 요소 개수)
int is_min_heap(PatientNode arr[], int len) {
    if (len == 0) return 1; // 빈 힙은 최소 힙으로 간주

    // 내부 노드들만 검사 (인덱스 1부터 len/2까지)
    for (int i = 1; i <= len / 2; i++) {
        // 왼쪽 자식이 존재하고, 부모가 왼쪽 자식보다 크면 최소 힙 아님
        if (LEFT_CHILD(i) <= len && arr[i].priority > arr[LEFT_CHILD(i)].priority) {
            printf("Min-heap violation: Parent P%d (prio %d) > Left Child P%d (prio %d) at index %d\n",
                   arr[i].patient_id, arr[i].priority,
                   arr[LEFT_CHILD(i)].patient_id, arr[LEFT_CHILD(i)].priority, i);
            return 0; // 최소 힙 조건 위반
        }
        // 오른쪽 자식이 존재하고, 부모가 오른쪽 자식보다 크면 최소 힙 아님
        if (RIGHT_CHILD(i) <= len && arr[i].priority > arr[RIGHT_CHILD(i)].priority) {
            printf("Min-heap violation: Parent P%d (prio %d) > Right Child P%d (prio %d) at index %d\n",
                   arr[i].patient_id, arr[i].priority,
                   arr[RIGHT_CHILD(i)].patient_id, arr[RIGHT_CHILD(i)].priority, i);
            return 0; // 최소 힙 조건 위반
        }
    }
    return 1; // 모든 노드가 최소 힙 조건을 만족
}

레퍼런스

“이 글은 『쉽게 배우는 C 자료구조』(최영규 및 천인국, 2024)의 내용을 토대로 재구성된 자료입니다.”​