그래프
그래프(Graph)
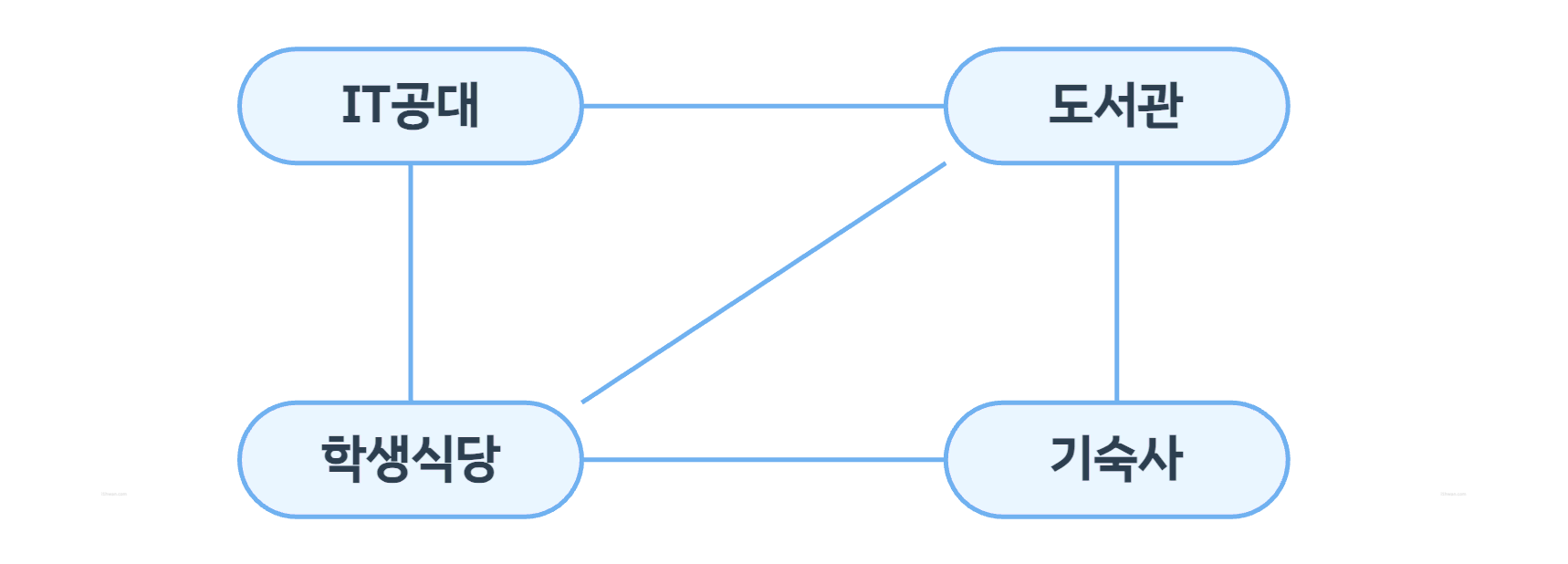
- 그래프(Graph): 연결되어 있는 객체 간의 관계를 표현하는 자료구조
- 가장 일반적인 자료구조 형태
그래프의 기본 구성
- 그래프 G: 객체를 나타내는 정점 또는 노드와 객체들을 연결하는 간선 또는 링크의 집합
- 정점 (Vertex): 여러 가지 특성을 가질 수 있는 객체 (ex: 도시, 사람, 웹페이지)
- 간선 (Edge): 정점들 간의 관계 (ex: 도로, 친구 관계, 하이퍼링크)
- $G = (V, E)$ 로 나타낼 수 있음
- $V$: 그래프에 있는 정점들의 집합
- $E$: 정점을 연결하는 간선들의 집합
⚠️
시각적으로 다르게 보이더라도, 정점들의 집합과 그 정점들을 연결하는 간선들의 집합이 동일하면 같은 그래프이다.
그래프의 종류
무방향 그래프 (Undirected Graph)
- 간선에 방향이 없는 그래프
- 정점 A와 정점 B를 연결하는 간선: $(A, B)$로 표현
- $(A, B) = (B, A)$: 간선의 양 끝 정점 순서가 중요하지 않음
방향 그래프 (Directed Graph)
- 간선에 방향이 있는 그래프
- 정점 A에서 정점 B를 연결하는 간선 (A → B): <A, B>로 표현
- $<A, B> \neq <B, A>$: 간선의 시작 정점과 끝 정점 순서가 중요
가중치 그래프 (Weighted Graph)
- 간선에 가중치(Weight), 비용(Cost)이 할당된 그래프
- 네트워크(Network)라고도 함
- 수학적 표현법
- $G = (V, E, w)$
- $V(G)$: 그래프 G의 정점들의 집합
- $E(G)$: 그래프 G의 간선들의 집합
- $w(e)$: 간선 e의 가중치 (강도, 비용, 길이 등)
완전 그래프 (Complete Graph)
- 모든 정점이 다른 모든 정점과 연결되어 있는 그래프
- 즉, 각 정점에서 다른 모든 정점을 연결하여 최대로 많은 간선 수를 가진 그래프
- 무방향 완전 그래프 (정점 n개): 최대 간선 수 = $n * (n-1) / 2$개
- 방향 완전 그래프 (정점 n개): 최대 간선 수 = $n * (n-1)$개
부분 그래프 (Subgraph)
- 원래 그래프에서 정점이나 간선을 일부만 제외하여 만든 그래프
그래프의 용어
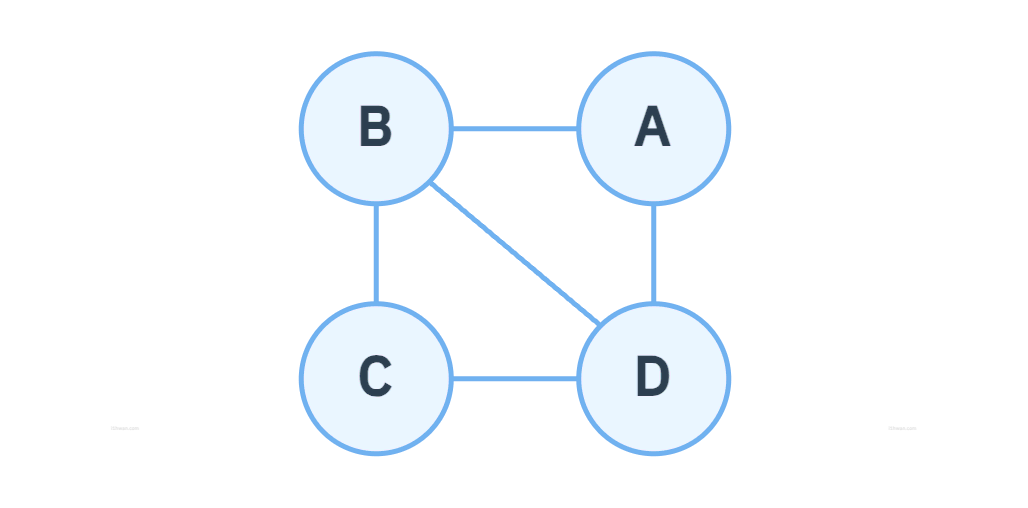
- 인접 정점 (Adjacent Vertex): 하나의 정점에서 간선에 의해 직접 연결된 정점
- 차수 (Degree): 하나의 정점에 연결되어 있는 다른 정점의 수
- 무방향 그래프
- 위의 무방향 그래프 G1에서 정점 B의 차수는 3
- 전체 차수: $간선 수 * 2$
- 방향 그래프
- 진입 차수 (In-degree): 정점을 머리(화살표 끝)로 하는 간선의 수 (해당 정점으로 들어오는 간선 수)
- 진출 차수 (Out-degree): 정점을 꼬리(화살표 시작)로 하는 간선의 수 (해당 정점에서 나가는 간선 수)
- 전체 차수: 진입 차수 + 진출 차수
- 전체 간선 수: 모든 진입 차수의 합 = 모든 진출 차수의 합
- 무방향 그래프
- 그래프의 경로 (Path): 그래프에서 간선을 따라갈 수 있는 길을 순서대로 나열한 것. 즉, 정점 s에서 정점 e까지 간선으로 연결된 정점들을 순서대로 나열한 리스트
- 무방향 그래프의 경로 (정점 s에서 e까지)
- 정점의 나열: s, v1, v2, ..., vk, e
- 반드시 간선 (s, v1), (v1, v2), ..., (vk, e)가 존재해야 함
- 무방향 그래프의 경로 (정점 s에서 e까지)
- 위의 그래프 G1에서 정점 A에서 정점 C까지의 경로는 A-B-C, A-B-D-C, A-D-C, A-D-B-C 등이 가능
- 방향 그래프의 경로 (정점 s에서 e까지)
- 정점의 나열: s, v1, v2, ..., vk, e
- 반드시 간선 <s, v1>, <v1, v2>, ..., <vk, e>가 존재해야 함
- 경로의 길이 (Length): 경로를 구성하는 데 사용된 간선의 수
- 단순 경로 (Simple Path): 경로 중에서 반복되는 간선이 없는 경로
- 사이클 (Cycle): 단순 경로 중에서 경로의 시작 정점과 마지막 정점이 동일한 경로
- 연결 그래프 (Connected Graph): 서로 다른 모든 쌍의 정점들 사이에 경로가 있는 그래프 (떨어져 있는 정점이 없는 그래프)
- 트리 (Tree): 그래프의 특수한 형태로, 사이클을 가지지 않는 연결 그래프[[1]]
[[1]]: 사이클이 없으면 임의의 두 정점을 연결하는 경로는 오직 하나이므로 트리를 만족한다.
그래프의 추상 자료형
- 데이터: 정점의 집합과 간선의 집합
- 연산
is_empty(): 그래프가 공백 상태인지 검사insert_vertex(v): 그래프에 정점 $v$를 삽입insert_edge(u, v): 그래프에 간선 ($u$, $v$)를 삽입delete_vertex(v): 정점 $v$를 그래프에서 삭제delete_edge(u, v): 간선 ($u$, $v$)를 그래프에서 삭제adjacent(v): 정점 $v$의 모든 인접 정점을 반환degree(v): 정점 $v$의 차수를 반환
그래프 구현
인접 행렬
- 그래프의 두 정점을 연결한 간선의 유무를 행렬로 저장
- $n$개의 정점을 가진 그래프: $n * n$ 행렬 이용
- 두 정점 i, j가 인접(연결)되어 있으면 M[i][j] = 1
- 인접되어 있지 않으면 M[i][j] = 0
- 대각선은 M[i][i] = 0
- 무방향 그래프의 인접 행렬
- 인접 행렬이 대칭 (M[i][j] = M[j][i])
- 행 i의 합 = 열 i의 합 = 정점 i의 차수
- 방향 그래프의 인접 행렬
- 행 i의 합 = 정점 i의 진출 차수
- 열 i의 합 = 정점 i의 진입 차수
#include <stdio.h>
#define MAX_USERS 5 // 최대 사용자 수
// 사용자 이름 (정점 데이터)
char user_names[MAX_USERS][20] = {"Alice", "Bob", "Charlie", "David", "Eve"};
// 친구 관계 (인접 행렬), 1이면 친구, 0이면 아님
int friendship_matrix[MAX_USERS][MAX_USERS] = {
{0, 1, 1, 0, 0}, // Alice: Bob, Charlie와 친구
{1, 0, 0, 1, 0}, // Bob: Alice, David와 친구
{1, 0, 0, 0, 1}, // Charlie: Alice, Eve와 친구
{0, 1, 0, 0, 1}, // David: Bob, Eve와 친구
{0, 0, 1, 1, 0} // Eve: Charlie, David와 친구
};
int num_users = 5; // 현재 사용자 수
// 특정 사용자의 친구 수 (차수)를 계산하는 함수
int get_friend_count(int user_index) {
int count = 0;
if (user_index < 0 || user_index >= num_users) {
printf("잘못된 사용자 인덱스입니다.\n");
return -1;
}
for (int i = 0; i < num_users; i++) {
if (friendship_matrix[user_index][i] == 1) {
count++;
}
}
return count;
}
// 두 사용자가 친구인지 확인하는 함수
int are_friends(int user1_index, int user2_index) {
if (user1_index < 0 || user1_index >= num_users ||
user2_index < 0 || user2_index >= num_users) {
printf("잘못된 사용자 인덱스입니다.\n");
return 0;
}
return friendship_matrix[user1_index][user2_index];
}
int main() {
printf("%s의 친구 수: %d\n", user_names[0], get_friend_count(0)); // Alice의 친구 수
printf("%s와 %s는 친구인가? %s\n", user_names[1], user_names[3],
are_friends(1, 3) ? "예" : "아니오"); // Bob과 David는 친구인가?
printf("%s와 %s는 친구인가? %s\n", user_names[0], user_names[4],
are_friends(0, 4) ? "예" : "아니오"); // Alice와 Eve는 친구인가?
return 0;
}
인접 리스트
- 그래프의 각 정점마다 자신과 인접한 정점들을 연결하여 만든 단순 연결 리스트
- 구조
- 헤드 포인터: 전체 정점의 개수만큼의 크기를 갖는 포인터 배열로 구성
- 노드: 각 인접 리스트의 노드는 정점 번호를 저장하는 필드와 다음 인접 정점을 연결하는 링크 필드로 구성
- 무방향 그래프의 특징 ($n$개 정점, $e$개 간선)
- 총 노드의 수: $2e$ (간선 (u, v)는 u의 리스트와 v의 리스트에 각각 한 번씩, 총 두 번 기록)
- 리스트의 길이: 한 정점의 인접 리스트에 연결된 노드의 수는 해당 정점의 차수
- 방향 그래프의 특징 ($n$개 정점, $e$개 간선)
- 총 노드의 수: $e$ (간선 <u, v>는 시작 정점 u의 리스트에만 기록)
- 리스트의 길이: 한 정점의 인접 리스트에 연결된 노드의 수는 해당 정점의 진출 차수
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX_PAGES 5 // 최대 웹페이지 수
// 인접 리스트의 노드 구조
typedef struct PageNode {
int page_id; // 연결된 페이지의 ID
struct PageNode* next_link; // 다음 연결된 페이지를 가리키는 포인터
} PageNode;
// 웹페이지 이름 (정점 데이터)
char page_urls[MAX_PAGES][50] = {"index.html", "about.html", "products.html", "contact.html", "blog.html"};
// 인접 리스트 (각 페이지에서 링크된 다른 페이지들)
PageNode* adj_list[MAX_PAGES];
int num_pages = 0;
// 그래프 초기화 (모든 인접 리스트를 NULL로)
void init_web_graph() {
num_pages = 0;
for (int i = 0; i < MAX_PAGES; i++) {
adj_list[i] = NULL;
}
}
// 새 웹페이지 추가 (실제로는 정점 번호만 관리)
void add_web_page(const char* url) {
if (num_pages >= MAX_PAGES) {
printf("Error: 최대 페이지 수 초과\n");
return;
}
// strcpy(page_urls[num_pages], url); // URL 저장
num_pages++;
}
// 페이지 from_id에서 페이지 to_id로의 링크 추가 (단방향)
void add_hyperlink(int from_id, int to_id) {
if (from_id < 0 || from_id >= num_pages || to_id < 0 || to_id >= num_pages) {
printf("Error: 잘못된 페이지 ID입니다.\n");
return;
}
PageNode* newNode = (PageNode*)malloc(sizeof(PageNode));
if (!newNode) {
printf("Memory allocation error\n");
return;
}
newNode->page_id = to_id;: 새 노드에 연결 대상 페이지 ID 저장
newNode->next_link = adj_list[from_id];: 새 노드의 다음 링크를 기존 from_id의 인접 리스트 헤드로 설정
adj_list[from_id] = newNode;: from_id의 인접 리스트 헤드를 새 노드로 변경 (리스트 앞에 삽입)
}
// 특정 페이지에서 나가는 링크들 출력
void print_outgoing_links(int page_id) {
if (page_id < 0 || page_id >= num_pages) {
printf("잘못된 페이지 ID입니다.\n");
return;
}
printf("%s 에서 나가는 링크: ", page_urls[page_id]);
PageNode* curr = adj_list[page_id];
while (curr != NULL) {
printf("%s ", page_urls[curr->page_id]);
curr = curr->next_link;
}
printf("\n");
}
// main 예시
int main_web_graph() {
init_web_graph();
add_web_page("index.html"); // 페이지 0
add_web_page("about.html"); // 페이지 1
add_web_page("products.html"); // 페이지 2
add_web_page("contact.html"); // 페이지 3
add_hyperlink(0, 1); // index.html -> about.html
add_hyperlink(0, 2); // index.html -> products.html
add_hyperlink(1, 0); // about.html -> index.html (역링크)
add_hyperlink(2, 3); // products.html -> contact.html
print_outgoing_links(0);
print_outgoing_links(1);
print_outgoing_links(2);
return 0;
}
인접 행렬과 인접 리스트 비교
| 특징 | 인접 행렬 (Adjacency Matrix) | 인접 리스트 (Adjacency List) |
|---|---|---|
| 메모리 공간 | 항상 $n^2$개의 공간 필요. 조밀 그래프(Dense Graph)에 효과적 (간선이 많을 때) | $n + 2e$(무방향)또는 $n + e$(방향)개의 공간 필요. 희소 그래프(Sparse Graph)에 효과적 (간선이 적을 때) |
| 간선 ($u$, $v$) 유무 확인 | adj[u][v] 직접 접근 $O(1)$ |
정점 $u$의 연결 리스트 전체 탐색. 정점 $u$의 차수를 $d_u$라 할 때 $O(d_u)$ |
| 정점 $v$의 차수 계산 | 행 $v$(또는 열 $v$)의 모든 성분 조사 $O(n)$ | 정점 $v$의 연결 리스트 길이 차수에 비례 $O(d_v)$ |
| 모든 인접 정점 탐색 | 해당 행의 모든 요소 조사 $O(n)$ | 해당 정점의 연결 리스트 모든 요소 방문 $O(d_v)$ |
| 전체 간선 수 파악 | 인접 행렬 전체 조사 $O(n^2)$ | 모든 인접 리스트의 모든 요소 방문 $O(n+e)$ |
- 조밀 그래프 (간선이 많음): 인접 행렬이 공간 효율성 및 특정 연산(간선 유무 확인)에서 유리할 수 있음
- 희소 그래프 (간선이 적음): 인접 리스트가 공간 효율성에서 압도적으로 유리하며, 많은 그래프 알고리즘에서 더 나은 성능을 보임
그래프 탐색
- 하나의 정점에서 시작하여 차례대로 그래프에 있는 모든 정점들을 한 번씩 방문하여 처리하는 연산
- 많은 문제들이 단순히 그래프 탐색만으로 해결됨
깊이 우선 탐색 (DFS: Depth First Search)
- 시작 정점에서 출발하여 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이 탐색
- 더 이상 갈 곳이 없으면, 가장 마지막에 만났던 갈림길(간선이 있는 정점)로 되돌아와 다른 방향의 간선으로 탐색을 계속 반복
- 가장 마지막에 만났던 갈림길의 정점으로 가장 먼저 되돌아가서 다시 깊이 우선 탐색을 반복해야 하므로, 후입선출(LIFO) 구조의 스택(Stack)[[2]] 사용
[[2]]: 실제 구현에서는 재귀 함수 호출을 통해 묵시적인 시스템 스택을 이용하는 경우가 많다.
- 시간 복잡도 ($n$은 정점의 수, $e$는 간선의 수)
- 인접 행렬 사용 시: $O(n^2)$
- 인접 리스트 사용 시: $O(n+e)$
// DFS 폴더 탐색
#include <stdio.h>
#include <stdbool.h>
#define MAX_NODES 7 // 예시 폴더/파일 수
// A(0) -> B(1), C(2)
// B(1) -> D(3), E(4)
// C(2) -> F(5)
// D, E, F, G(6)는 파일 (더 이상 하위 폴더 없음)
int adj_matrix[MAX_NODES][MAX_NODES] = {
{0,1,1,0,0,0,0}, // A
{0,0,0,1,1,0,0}, // B
{0,0,0,0,0,1,0}, // C
{0,0,0,0,0,0,0}, // D
{0,0,0,0,0,0,0}, // E
{0,0,0,0,0,0,0}, // F
{0,0,0,0,0,0,0} // G (연결 없음 예시)
};
char node_names[MAX_NODES][10] = {"FolderA", "FolderB", "FolderC", "FileD", "FileE", "FileF", "FileG"};
bool visited[MAX_NODES];
int num_nodes = MAX_NODES;
void dfs_explore_folders(int current_node_idx) {
visited[current_node_idx] = true;: 현재 폴더/파일(current_node_idx)을 방문했다고 표시
printf("방문: %s\n", node_names[current_node_idx]);
for (int i = 0; i < num_nodes; i++) {
// 현재 노드에서 i번 노드로 가는 간선이 있고 (adj_matrix[current_node_idx][i] == 1)
// 아직 i번 노드를 방문하지 않았다면 (visited[i] == false)
if (adj_matrix[current_node_idx][i] == 1 && !visited[i]) {
dfs_explore_folders(i); // 하위 폴더/파일(i)로 재귀적 탐색
}
}
}
int main_dfs() {
for (int i = 0; i < num_nodes; i++) {
visited[i] = false; // 방문 배열 초기화
}
printf("--- DFS 폴더 탐색 시작 (FolderA부터) ---\n");
dfs_explore_folders(0); // 0번 노드(FolderA)에서 탐색 시작
return 0;
}
너비 우선 탐색 (BFS: Breadth First Search)
- 시작 정점에서 가장 가까운 거리에 있는 이웃 정점들을 먼저 모두 탐색
- 그 후, 탐색했던 정점들의 이웃들을 다시 순서대로 방문하는 방식으로 점차 탐색 범위를 넓힘
- 먼저 발견한 정점의 이웃을 먼저 탐색해야 하므로, 선입선출(FIFO) 구조의 큐(Queue) 사용
- 시간 복잡도 ($n$은 정점의 수, $e$는 간선의 수)
- 인접 행렬 사용 시: $O(n^2)$
- 인접 리스트 사용 시: $O(n+e)$
// 친구의 친구 찾기
#include <stdio.h>
#include <stdbool.h>
#define MAX_USERS_BFS 6 // 예시 사용자 수
// 0(나) -> 1(A), 2(B) (1촌)
// 1(A) -> 3(C)
// 2(B) -> 4(D), 5(E)
// C, D, E는 2촌
int adj_matrix_bfs[MAX_USERS_BFS][MAX_USERS_BFS] = {
{0,1,1,0,0,0}, // 나
{1,0,0,1,0,0}, // A
{1,0,0,0,1,1}, // B
{0,1,0,0,0,0}, // C
{0,0,1,0,0,0}, // D
{0,0,1,0,0,0} // E
};
char user_names_bfs[MAX_USERS_BFS][10] = {"Me", "Alice", "Bob", "Charlie", "David", "Eve"};
bool visited_bfs[MAX_USERS_BFS];
int queue[MAX_USERS_BFS];
int front = -1, rear = -1;
int num_users_bfs = MAX_USERS_BFS;
void enqueue(int user_id) {
if (rear == MAX_USERS_BFS - 1) return; // 큐가 꽉 참
if (front == -1) front = 0;
rear++;
queue[rear] = user_id;
}
int dequeue() {
if (front == -1 || front > rear) return -1; // 큐가 비었거나 모든 요소 처리
int user_id = queue[front];
front++;
return user_id;
}
bool is_queue_empty() {
return (front == -1 || front > rear);
}
void bfs_find_friends(int start_user_idx) {
for (int i = 0; i < num_users_bfs; i++) {
visited_bfs[i] = false;
}
front = rear = -1; // 큐 초기화
visited_bfs[start_user_idx] = true;: 시작 사용자(start_user_idx)를 방문했다고 표시
printf("방문: %s (시작점)\n", user_names_bfs[start_user_idx]);
enqueue(start_user_idx);: 시작 사용자를 큐에 추가
while (!is_queue_empty()) {
int current_user_idx = dequeue(); // 큐에서 사용자 한 명을 꺼냄
for (int i = 0; i < num_users_bfs; i++) {
// 현재 사용자와 i번 사용자가 친구이고 (adj_matrix_bfs[current_user_idx][i] == 1)
// 아직 i번 사용자를 방문하지 않았다면 (visited_bfs[i] == false)
if (adj_matrix_bfs[current_user_idx][i] == 1 && !visited_bfs[i]) {
visited_bfs[i] = true;: i번 사용자를 방문했다고 표시
printf("방문: %s (인접 사용자)\n", user_names_bfs[i]);
enqueue(i);: i번 사용자를 큐에 추가하여 나중에 탐색
}
}
}
}
int main_bfs() {
printf("--- BFS 친구 관계 탐색 시작 (Me부터) ---\n");
bfs_find_friends(0); // 0번 사용자(Me)에서 탐색 시작
return 0;
}
신장 트리 (Spanning Tree)
- 그래프의 모든 정점을 최소한의 간선으로 연결하는 트리
- 모든 정점들이 연결되어야 하고, 사이클을 포함하면 안됨
- $n$개의 정점을 갖는 그래프의 신장 트리는 항상 $n-1$개의 간선을 가짐
- 하나의 그래프에는 다양한 신장 트리가 존재할 수 있음
- 최소의 링크(간선)를 사용하는 네트워크 구축 시 사용
#include <stdio.h>
#include <stdbool.h>
#define MAX_CITIES_ST 5
// A(0)-B(1), A(0)-C(2), B(1)-D(3), C(2)-D(3), C(2)-E(4), D(3)-E(4)
int road_network[MAX_CITIES_ST][MAX_CITIES_ST] = {
{0,1,1,0,0}, // A
{1,0,0,1,0}, // B
{1,0,1,1,1}, // C
{0,1,1,0,1}, // D
{0,0,1,1,0} // E
};
char city_names_st[MAX_CITIES_ST][10] = {"CityA", "CityB", "CityC", "CityD", "CityE"};
bool visited_st[MAX_CITIES_ST];
int num_cities_st = MAX_CITIES_ST;
// DFS를 이용하여 신장 트리의 간선을 출력하는 함수
// parent_city_idx는 현재 city_idx로 오게 된 부모 노드를 의미 (사이클 방지 및 간선 식별용)
void spanning_tree_by_dfs(int current_city_idx, int parent_city_idx) {
visited_st[current_city_idx] = true;
for (int neighbor_city_idx = 0; neighbor_city_idx < num_cities_st; neighbor_city_idx++) {
if (road_network[current_city_idx][neighbor_city_idx] == 1) { // 연결된 도시이고
if (!visited_st[neighbor_city_idx]) { // 아직 방문하지 않은 이웃 도시라면
// 이것이 신장 트리의 간선이 됨
printf("신장 트리 간선: %s - %s\n", city_names_st[current_city_idx], city_names_st[neighbor_city_idx]);
spanning_tree_by_dfs(neighbor_city_idx, current_city_idx);
}
// else if (neighbor_city_idx != parent_city_idx) {
// // 이미 방문했고, 부모가 아니라면 사이클을 형성하는 간선 (신장 트리에는 포함 안 됨)
// }
}
}
}
int main_st_dfs() {
for (int i = 0; i < num_cities_st; i++) {
visited_st[i] = false;
}
printf("--- DFS 기반 신장 트리 간선 탐색 (CityA부터) ---\n");
spanning_tree_by_dfs(0, -1); // 0번 도시(CityA)에서 시작, 부모 없으므로 -1
return 0;
}
최소 비용 신장 트리 (MST)
- 무방향 가중치 그래프에서 신장 트리를 구성하는 간선들의 가중치 합이 최소인 신장 트리
최소 비용 신장 트리 조건
- 그리프의 모든 정점을 포함
- 간선의 가중치의 합이 최소
- 사이클을 포함하지 않고, 반드시 ($n-1$)개의 간선만 사용
최소 비용 신장 트리를 만드는 알고리즘
Prim 알고리즘
- 간선을 미리 정렬하지 않고, 하나의 정점에서부터 MST를 단계적으로 확장하는 방법
- 과정
- 처음에는 시작 정점만이 신장 트리 집합에 포함됨
- 현재의 신장 트리 집합에 인접한 정점 중 최저 가중치의 간선으로 연결된 정점을 선택하여 신장 트리 집합에 추가
- 이 과정을 $n-1$개의 간선을 가질 때까지 반복
- 시간 복잡도: $O(n^2)$ (인접 행렬 사용 시)
- 정점의 수가 적은 조밀 그래프에서 유리
#include <stdio.h>
#include <stdbool.h>
#include <limits.h> // INT_MAX 사용
#define MAX_CITIES_PRIM 5
#define INF INT_MAX // 무한대 값
// 도시 간 케이블 설치 비용 (가중치 인접 행렬)
// A B C D E
int cable_costs[MAX_CITIES_PRIM][MAX_CITIES_PRIM] = {
{0, 2, 0, 6, 0}, // A
{2, 0, 3, 8, 5}, // B
{0, 3, 0, 0, 7}, // C
{6, 8, 0, 0, 9}, // D
{0, 5, 7, 9, 0} // E
};
// 간선 없는 곳은 INF로 표현해야 하지만, 여기서는 0으로 두고 코드 내에서 처리
// 실제 Prim에서는 INF로 초기화된 dist 배열을 사용
char city_names_prim[MAX_CITIES_PRIM][10] = {"A", "B", "C", "D", "E"};
int num_cities_prim = MAX_CITIES_PRIM;
void prim_mst() {
int dist[MAX_CITIES_PRIM]; // 시작 정점으로부터 각 정점까지의 최소 간선 가중치
bool selected[MAX_CITIES_PRIM]; // MST에 포함된 정점인지 여부
int parent[MAX_CITIES_PRIM]; // MST에서 각 정점의 부모 정점 (경로 추적용)
int total_min_cost = 0;
// 초기화
for (int i = 0; i < num_cities_prim; i++) {
dist[i] = INF;: 모든 도시까지의 거리를 무한대로 초기화
selected[i] = false;: 어떤 도시도 아직 MST에 선택되지 않음으로 표시
parent[i] = -1;
}
dist[0] = 0; // 시작 정점(A, 인덱스 0)의 거리는 0
printf("Prim 알고리즘 MST 간선:\n");
for (int count = 0; count < num_cities_prim - 1; count++) {
// MST에 포함되지 않은 정점 중에서 최소 dist 값을 갖는 정점 u 찾기
int min_dist = INF;
int u = -1;
for (int v_idx = 0; v_idx < num_cities_prim; v_idx++) {
if (!selected[v_idx] && dist[v_idx] < min_dist) {
min_dist = dist[v_idx];
u = v_idx;
}
}
if (u == -1) { // 연결 그래프가 아닌 경우
printf("MST를 구성할 수 없습니다 (연결 그래프가 아님).\n");
return;
}
selected[u] = true;: 찾은 정점 u를 MST에 포함시킴
if (parent[u] != -1) { // 시작 정점이 아닌 경우에만 간선 출력
printf("%s - %s (비용: %d)\n", city_names_prim[parent[u]], city_names_prim[u], cable_costs[u][parent[u]]);
}
total_min_cost += dist[u];
// 선택된 정점 u에 인접한 정점들의 dist 값 갱신
for (int v_adj = 0; v_adj < num_cities_prim; v_adj++) {
// u와 v_adj 사이에 간선이 있고 (cable_costs[u][v_adj] != 0),
// v_adj가 아직 MST에 포함되지 않았으며 (selected[v_adj] == false),
// u를 통해 v_adj로 가는 비용이 현재 dist[v_adj]보다 작으면 갱신
if (cable_costs[u][v_adj] != 0 && !selected[v_adj] && cable_costs[u][v_adj] < dist[v_adj]) {
parent[v_adj] = u;: v_adj의 부모를 u로 설정
dist[v_adj] = cable_costs[u][v_adj];: v_adj까지의 최소 비용을 갱신
}
}
}
// 실제 total_min_cost는 dist 배열의 합이 아니라, 선택된 간선들의 가중치 합으로 계산해야 함
// 위의 코드에서는 dist[u]를 더하고 있으나, 이는 시작점으로부터의 거리이므로,
// 실제 MST의 총 비용은 선택된 간선들의 가중치 합으로 다시 계산하는 것이 정확.
// 여기서는 간선 출력 시 비용을 함께 보여주는 것으로 대체.
// 정확한 총 비용 계산:
total_min_cost = 0;
for(int i=1; i<num_cities_prim; ++i){ // 시작 정점 제외
if(parent[i] != -1) total_min_cost += cable_costs[i][parent[i]];
}
printf("최소 총 케이블 설치 비용: %d\n", total_min_cost);
}
int main_prim() {
prim_mst();
return 0;
}
Kruskal 알고리즘
- 모든 간선을 가중치 순으로 정렬한 뒤, 사이클을 만들지 않는 간선 중에서 가장 가중치가 작은 간선부터 순서대로 $n-1$개를 선택
- 과정
- 모든 간선을 가중치에 따라 오름차순으로 정렬
- 사이클을 만들지 않는 간선[[3]] 중 가중치가 가장 낮은 간선부터 차례대로 선택
- $n-1$개의 간선이 선택될때 까지 반복
- 시간 복잡도: $O(e\log{e})$ (e는 간선의 수)
- 대부분 시간은 간선들을 가중치에 따라 정렬하는 데 소요됨
- 간선의 수가 적은 희소 그래프에서는 Prim보다 Kruskal 알고리즘이 유리
[[3]]: 사이클이 생기는지 여부는 Union-Find 알고리즘으로 판별한다.
#include <stdio.h>
#include <stdlib.h> // qsort, malloc
#define MAX_SITES_KRUSKAL 5
#define MAX_ROADS_KRUSKAL 10 // 최대 간선 수 (캠핑장 수 * (캠핑장 수 - 1) / 2 보다 작거나 같음)
typedef struct Road {
int site1; // 캠핑장1 ID
int site2; // 캠핑장2 ID
int cost; // 도로 건설 비용
} Road;
char site_names_kruskal[MAX_SITES_KRUSKAL][20] = {"LakeView", "MountainTop", "RiverSide", "ForestHut", "SunnyMeadow"};
Road road_proposals[MAX_ROADS_KRUSKAL];
int num_sites_kruskal = 0;
int num_road_proposals = 0;
// Union-Find를 위한 parent 배열
int parent_kruskal[MAX_SITES_KRUSKAL];
// qsort를 위한 비교 함수
int compare_roads(const void* a, const void* b) {
Road* roadA = (Road*)a;
Road* roadB = (Road*)b;
return (roadA->cost - roadB->cost); // 비용 오름차순 정렬
}
// Find 연산 (경로 압축 적용 가능)
int find_set(int site_id) {
if (parent_kruskal[site_id] == site_id)
return site_id;
return parent_kruskal[site_id] = find_set(parent_kruskal[site_id]); // 경로 압축
}
// Union 연산
void union_sets(int site_id1, int site_id2) {
int root1 = find_set(site_id1);
int root2 = find_set(site_id2);
if (root1 != root2) {
parent_kruskal[root2] = root1; // root2를 root1의 자식으로 합침
}
}
void add_road_proposal(int s1, int s2, int c) {
if (num_road_proposals >= MAX_ROADS_KRUSKAL) return;
road_proposals[num_road_proposals].site1 = s1;
road_proposals[num_road_proposals].site2 = s2;
road_proposals[num_road_proposals].cost = c;
num_road_proposals++;
}
void kruskal_mst() {
// 1. 모든 간선을 비용 순으로 정렬
qsort(road_proposals, num_road_proposals, sizeof(Road), compare_roads);
// 2. 각 정점을 자신만을 포함하는 집합으로 초기화 (Union-Find 준비)
for (int i = 0; i < num_sites_kruskal; i++) {
parent_kruskal[i] = i;
}
int edges_accepted = 0;
int total_min_cost = 0;
printf("Kruskal 알고리즘 MST 간선:\n");
for (int i = 0; i < num_road_proposals; i++) {
if (edges_accepted == num_sites_kruskal - 1) break; // n-1개 간선 선택 완료
Road current_road = road_proposals[i];
// 3. 현재 간선이 사이클을 형성하는지 확인 (두 정점이 같은 집합에 속하는지)
if (find_set(current_road.site1) != find_set(current_road.site2)) {
// 사이클을 형성하지 않으면 MST에 추가
union_sets(current_road.site1, current_road.site2); // 두 집합을 합침
printf("%s - %s (비용: %d)\n", site_names_kruskal[current_road.site1], site_names_kruskal[current_road.site2], current_road.cost);
total_min_cost += current_road.cost;
edges_accepted++;
}
}
printf("최소 총 도로 건설 비용: %d\n", total_min_cost);
}
int main_kruskal() {
num_sites_kruskal = 5;
// (LakeView-0, MountainTop-1, RiverSide-2, ForestHut-3, SunnyMeadow-4)
add_road_proposal(0, 1, 10); // LakeView - MountainTop, 비용 10
add_road_proposal(0, 2, 20);
add_road_proposal(1, 2, 5);
add_road_proposal(1, 3, 15);
add_road_proposal(2, 3, 8);
add_road_proposal(2, 4, 25);
add_road_proposal(3, 4, 12);
kruskal_mst();
return 0;
}
최단 경로 (Shortest Path)
- 신장 트리가 아닌 가중치 그래프에서 정점 $u$와 정점 $v$를 연결하는 여러 경로 중에서 간선들의 가중치 합이 최소인 경로의 비용을 구하는 문제
- 간선의 가중치는 양수라고 가정
⚠️
음수인 간선이 있을때, 음수인 간선을 양수로 만들도록 동일한 값을 간선에 전부 더하면 안될까?
모든 간선에 동일한 값을 더해 가중치를 양수로 만드는 경우, 간선을 많이 거치는 경로일수록 동일하게 더했던 값이 누적되어 비용이 더 많이 늘어나기 때문이다. 이로 인해 원래 최단 경로가 아닌 다른 경로가 최단 경로로 바뀌는 문제가 생긴다.
모든 간선에 동일한 값을 더해 가중치를 양수로 만드는 경우, 간선을 많이 거치는 경로일수록 동일하게 더했던 값이 누적되어 비용이 더 많이 늘어나기 때문이다. 이로 인해 원래 최단 경로가 아닌 다른 경로가 최단 경로로 바뀌는 문제가 생긴다.
가중치 인접 행렬 (Weight Adjacency Matrix) for 최단 경로
- 최단 경로를 구하려는 가중치 그래프의 가중치를 저장
- 그래프에서 사용한 인접 행렬과 같은 형태의 2차원 배열 사용
- 두 정점 사이에 간선이 없으면 0이 아니라 ∞ (무한대) 값이 저장되어 있다고 가정
- 각 정점은 자기 자신과 이어진 간선을 허용하지 않으므로 (일반적인 경우), 가중치 인접 행렬에서 대각선 값은 0
Dijkstra 알고리즘
- 하나의 시작 정점에서 다른 모든 정점까지의 최단 경로를 구하는 알고리즘
- 음의 가중치가 없는 그래프에서 정상적으로 동작하며, 매 상황에서 가장 비용이 적은 노드를 선택하는 그리디 알고리즘
- 과정
- $S$: 최단 거리가 확정된 정점들의 집합. 처음에는 비어있음
- dist[]: 시작 정점 s로부터 각 정점까지의 현재까지 알려진 최단 거리 추정값
- $S$에 포함되지 않은 정점 중에서 dist 값이 최소인 정점 $v$를 찾음
- 정점 $v$까지의 거리를 확정하고, $v$를 집합 $S$에 추가
- 정점 $v$에 인접한 정점 $w$들에 대해, $v$를 거쳐 $w$로 가는 경로가 기존 dist[w]보다 짧다면 dist[w]를 갱신 (dist[w] = min(dist[w], dist[v] + cost(v,w)))
- 모든 정점이 S에 포함될 때까지 반복
- Dijkstra 알고리즘의 시간 복잡도: $O(n^2)$
Floyd-Warshall 알고리즘
- 모든 정점에서 다른 모든 정점까지의 최단 경로를 구함
- 과정
- 최단 경로 거리 행렬 $A$를 이용
- $A^k$[i][j]: 0부터 $k$까지의 정점만을 중간 경유지로 사용하여 정점 $i$에서 정점 $j$까지 가는 최단 경로의 길이
- $A^{-1}$ (초깃값): 그래프의 가중치 인접 행렬 (직접 연결된 간선의 가중치, 없으면 INF, 자신은 0)
- $A^{-1}$ → $A^0$ → $A^1$ → ... → $A^{n-1}$ 순으로 최단 경로를 구해나감
- 삼중 루프로 구성
- 바깥 루프 $k$: 경유지로 고려할 정점 ($0$부터 $n-1$까지)
- 중간 루프 $i$: 출발 정점
- 안쪽 루프 $j$: 도착 정점
- $k$를 거치지 않는 기존 $i$ → $j$ 최단 경로와, $k$를 거쳐가는 $i$ → $k$ 최단 경로 + $k$ → $j$ 최단 경로 중 더 짧은 것을 선택
- $A^k$[i][j] = min($A^{k-1}$[i][j], $A^{k-1}$[i][k] + $A^{k-1}$[k][j] )
- Floyd 알고리즘 시간 복잡도: $O(n^3)$
Dijkstra와 Floyd-Warshall 비교
- 모든 정점 쌍의 최단 경로를 구하려면, Dijkstra 알고리즘$O(n^2)$을 $n$번 반복하여 전체 복잡도 $O(n^3)$으로 해결할 수도 있음
- 두 알고리즘 모두 모든 쌍 문제에 대해 동일한 $O(n^3)$ 복잡도를 가지지만, Floyd 알고리즘은 코드가 매우 간결하고 이해하기 쉬운 장점이 있음.
레퍼런스
“이 글은 『쉽게 배우는 C 자료구조』(최영규 및 천인국, 2024)의 내용을 토대로 재구성된 자료입니다.”

