데이터의 저장
컴퓨터 시스템 계층 구조
- 컴퓨터 시스템은 여러 계층으로 구성됨
- 응용 소프트웨어: 사용자와 직접 상호작용
- 운영체제: 하드웨어 자원 관리 및 응용 소프트웨어 지원
- 컴퓨터 하드웨어: 물리적인 장치들
- CPU, 캐시 메모리, RAM 메모리, 디스크, 네트워크 장치, 키보드, 마우스, 디스플레이, 프린터 등
데이터의 저장
비트 (Binary digit)
- 컴퓨터 안에서 데이터나 정보는 2진수 0과 1의 패턴으로 표현됨 이를 데이터나 정보가 표현되는 기본 단위인 비트로 부름
- 숫자, 문자(한글, 알파벳, 특수문자), 이미지, 소리 등: 모두 비트 패턴들로 나타냄
- 비트 패턴 체계: 2진법, 8진법, 16진법, BCD, ASCII, Unicode 등
부울 연산 (Boolean operation)
- AND, OR, XOR(exclusive-OR) 연산
- 디지털 회로 설계, 데이터베이스 검색 엔진, 소프트웨어 알고리즘 등에 응용
논리 게이트와 플립플롭
논리 게이트 (logic gate)
부울 연산을 구현하는 전자장치
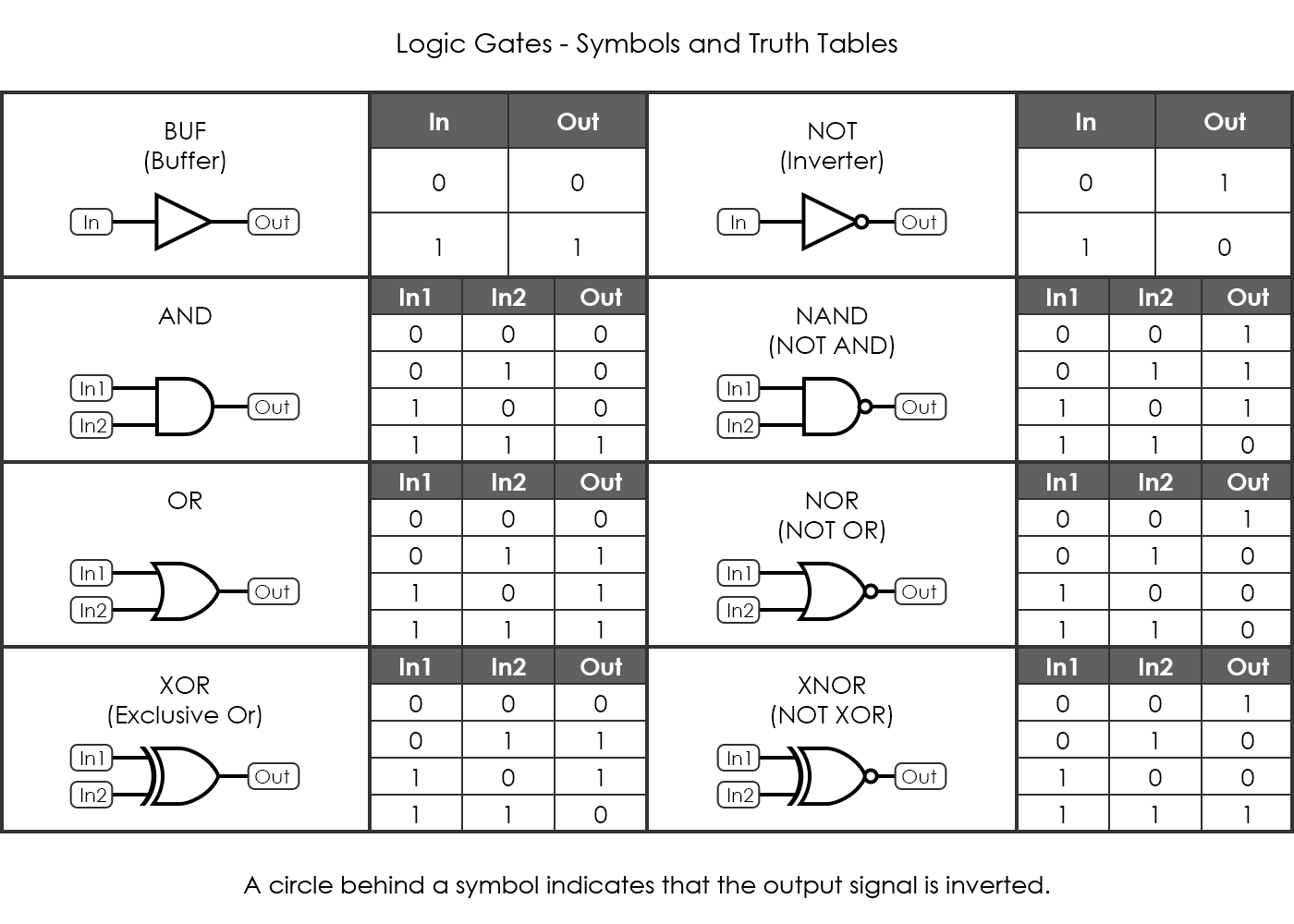
- 트랜지스터(transistor)와 저항으로 구현됨
- 입력 값 "0"과 "1"은 전압 수준으로 나타냄
- 디지털 회로를 설계할 때 사용되는 기본 단위임
플립플롭 (flip-flop)
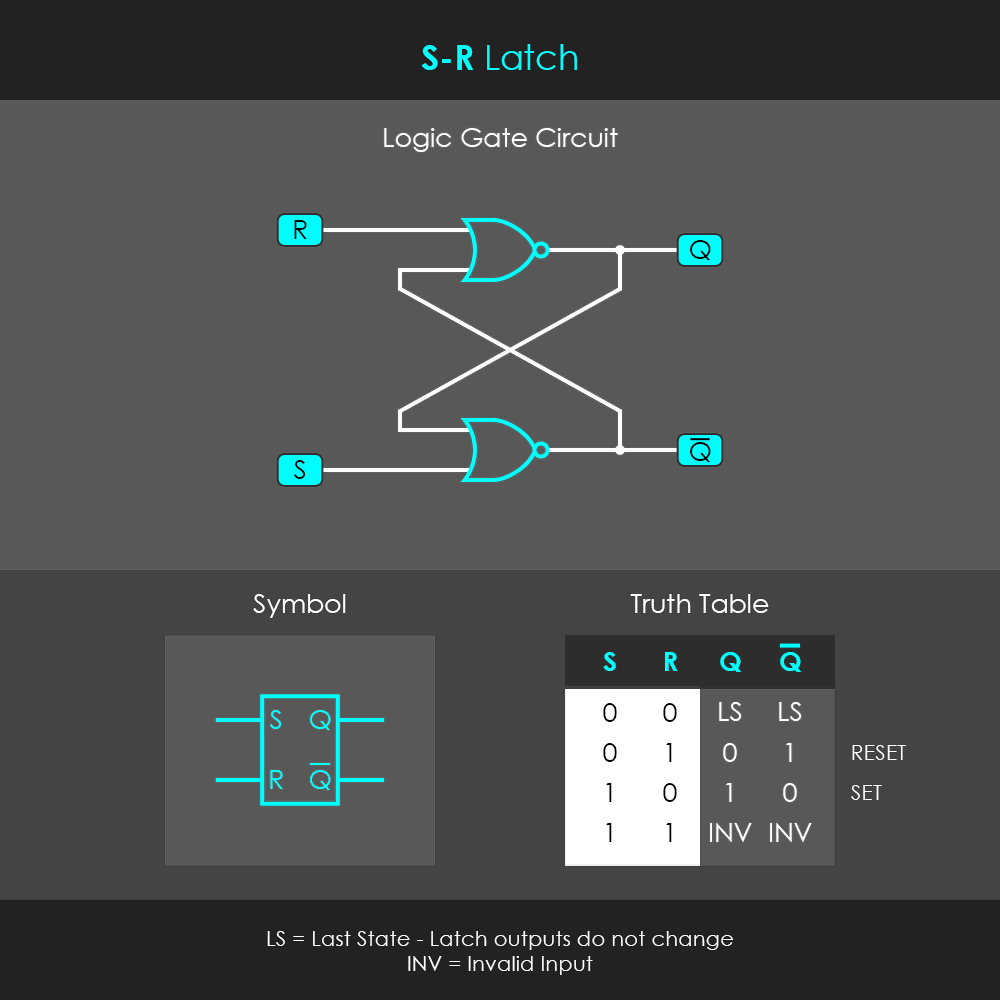
- 컴퓨터 메모리의 기본 단위, 레지스터(register), 캐시 메모리(SRAM)의 기본 소자
- 0 또는 1을 출력 값으로 가짐
- 다른 회로로부터 펄스 신호를 받아 출력 값을 변경하며, 그 전까지는 출력 값을 일정하게 유지하는 회로
주기억장치
- 주기억장치(memory)에 실행될 코드와 데이터가 저장됨
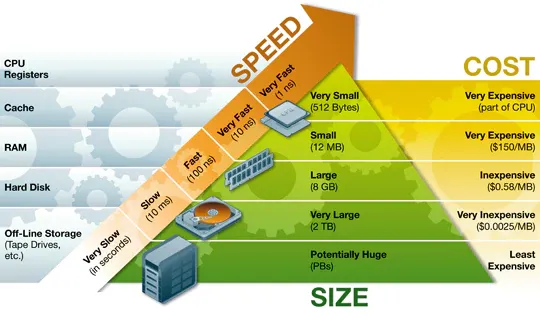
- 컴퓨터 하드웨어 구성과 기억장치 계층 구조: 레지스터 > 캐시 > 주기억장치 > 보조기억장치 순으로 속도가 빠르고 비트당 비용이 높으며 용량이 작음
메모리 구성
- 메모리의 기본 단위: 8비트의 묶음인 바이트(byte)
- 메모리는 바이트 크기 메모리 셀(cell)로 조직됨
- 상단(high-order end), 하단(low-order end)으로 구분
- 최상위 비트(MSB: Most Significant Bit), 최하위 비트(LSB: Least Significant Bit)
0 1 0 1 1 0 1 0 ↑ ↑ 최상위 비트 (MSB) 최하위 비트 (LSB)
- 주기억장치는 셀을 고유하게 식별함: 주소(address)
- 주소는 숫자를 사용하며 0부터 시작하는 일련번호임
- 셀 주소와 셀 안의 비트들에 순서를 부여할 수 있음: 더 큰 단위의 비트 패턴을 저장할 수 있음
- 메모리 셀 접근(access) 동작: 읽기 연산 / 쓰기 연산
RAM (Random Access Memory)
- 필요한 셀에 임의의 순서로/독립적으로 접근할 수 있으며, 각 셀에 접근하는 데 걸리는 시간은 동일함 (Random Access)
- 종류: DRAM(Dynamic RAM), SDRAM(Synchronous DRAM)
메모리 용량 단위
| 단위 | 바이트(2n) | 바이트(10n) |
|---|---|---|
| 킬로바이트 (KB) | 210 바이트 | 103 바이트 |
| 메가바이트 (MB) | 220 바이트 | 106 바이트 |
| 기가바이트 (GB) | 230 바이트 | 109 바이트 |
| 테라바이트 (TB) | 240 바이트 | 1012 바이트 |
| 페타바이트 (PB) | 250 바이트 | 1015 바이트 |
| 엑사바이트 (EB) | 260 바이트 | 1018 바이트 |
| 제타바이트 (ZB) | 270 바이트 | 1021 바이트 |
보조기억장치
- 비휘발성(non-volatile) 저장장치임 (전원이 꺼져도 내용 유지)
- 저장 비용이 적음
- 컴퓨터에서 분리하여 보관할 수 있음
- 하드 디스크(HDD), 자기 테이프, CD, 플래시 메모리(SSD) 등
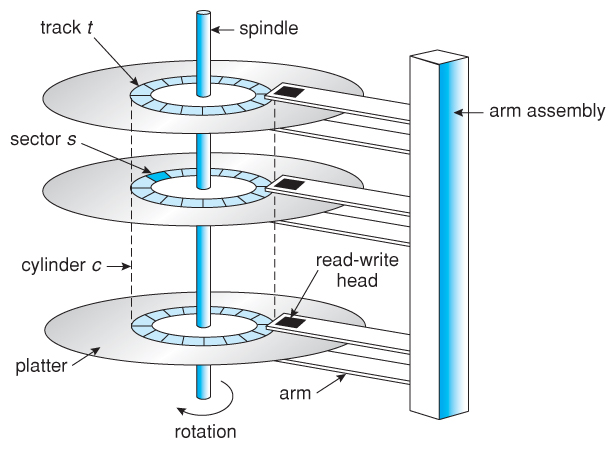
하드 디스크 (hard disk)
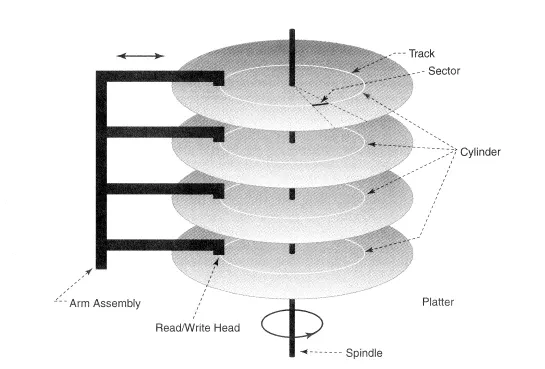
- 트랙(track): 데이터가 저장되는 플래터 표면상의 동심원
- 섹터(sector): 트랙을 일정한 크기로 나눈 것
- 디스크에 데이터를 한 번에 읽고/쓰는 최소의 단위
- 실린더(cylinder): 모든 플래터 표면상의 동일한 위치에 있는 동심원
디스크 성능 측정 매개변수
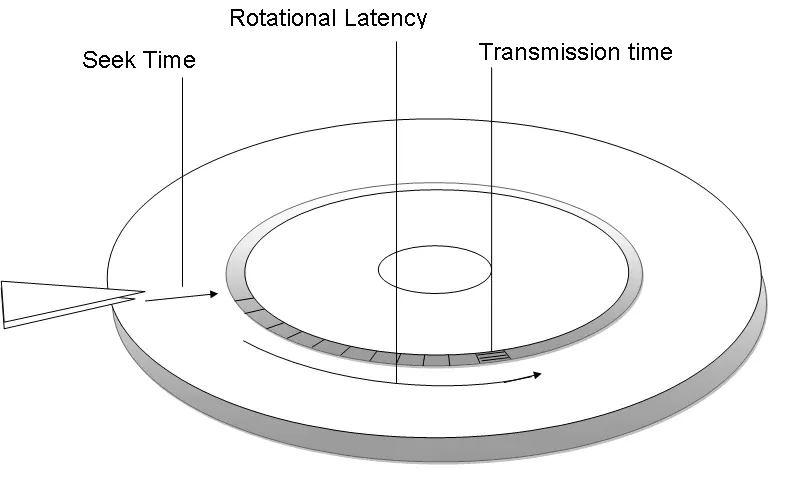
- 탐색 시간(seek time): 헤드를 액세스할 데이터가 저장된 트랙으로 이동시키는 데 걸리는 시간
- 회전 지연 시간(rotation latency time): 헤드를 해당 트랙에 위치시킨 후 디스크가 회전하여 원하는 섹터가 헤드 아래에 위치하는 데 걸리는 시간 (한 바퀴 도는 시간의 1/2)
- 데이터 전송 시간(data transfer time): 헤더가 액세스한 데이터를 전송하는 데 걸리는 시간
- 대역폭(bandwidth): 단위 시간 동안 전송될 수 있는 총 비트 수
디스크 포맷
| 구분 | 512바이트 섹터 | 4096바이트 섹터 |
|---|---|---|
| Gap, sync, address mark | 15바이트 | 15바이트 |
| 사용자 데이터 | 512바이트 | 4096바이트 |
| ECC | 50바이트 | 100바이트 |
| 총바이트 수 | 577바이트 | 4211바이트 |
| 효율 | 88.7% | 97.3% |
플래시 메모리
전기적으로 데이터를 기록하고 지울 수 있는 비휘발성 기억장치
- SSD(Solid State Drive) 등으로 사용됨
- 페이지 단위 쓰기, 블록 단위 지우기 특성 가짐
플래시 메모리 타입 및 특성 비교
| 구분 | NAND 타입 | NOR 타입 |
|---|---|---|
| 용도 | USB, SSD 등 저장 매체 | RAM처럼 실행 가능한 코드 저장 |
| 읽기 | 블록 단위 임의적 액세스 가능. 느림 | 셀 단위 임의적 액세스 가능. 빠름 |
| 쓰기 | 한 번에 한 블록을 기록함. 빠름 | 한 셀씩 기록하여 느림 |
| 밀도 | 고밀도 | 저밀도 |
| 가격 | 저가 | 고가 |
비트 패턴을 이용한 정보의 표현
- 데이터(data): 관찰이나 측정을 통해 수집한 사실이나 숫자
- 맥락 없이 단순히 나열된 값
- 예: 23, 45, 67
- 정보(information): 데이터를 처리하고 해석하여 유용한 의미나 지식을 제공하는 것
- 데이터에 맥락, 관련성 및 목적을 부여하여 의사 결정을 도움
- 예: "학생의 평균 점수는 45이다"
데이터와 정보의 예시
- 데이터: 월요일: 20 °C, 화요일: 22 °C, 수요일: 21 °C, 목요일: 23 °C ... (측정된 값 나열)
- 정보: 평균 기온, 기온 변화 패턴, 최고 기온과 최저 기온, 이후 경향 등 (해석된 의미)
텍스트 표현
- 텍스트 표현 원리: 텍스트상의 상이한 문자 각각에 고유한 비트 패턴(코드, code)을 지정함
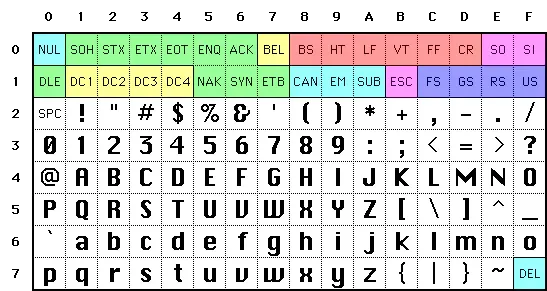
- 국제 표준 코딩 체계(ANSI, ISO): 다양한 언어의 표현, 통신에서 발생하는 문제 해결
- ASCII(American Standard Code for Information Interchange): 1 byte (영문, 숫자, 기호 등)
- 유니코드(Unicode): 일반적으로 2 byte (전 세계 대부분의 문자 표현 가능)
- 'A': U+0041, '가': U+AC00
- UTF-8(Unicode Transformation Format 8-bit): 1~4 byte (가변 길이 인코딩, ASCII와 호환)
- 텍스트 파일(.txt): ASCII나 Unicode를 사용하여 인코딩된 기호들로 구성된 파일
- 워드프로세서 파일(.docx, .hwpx): 문자별 코드, 폰트 변경, 서식, 열 맞춤 정보 등 추가적 구조를 포함
숫자 표현
- 숫자 표현 원리: 2진법, 16진법을 사용하여 표현함
- 16비트에 ASCII 코드로 표현할 수 있는 10진 숫자의 범위: 0 ~ 99 (문자 '0'부터 '9'까지 각각 표현)
- 16비트에 2진수로 표현할 수 있는 10진 양수의 범위: 0 ~ 65,535 $(2^{16} - 1)$
이미지 표현
- 비트맵(bitmap) 기법: 이미지를 픽셀(pixel)들의 집합으로 표현하는 방식
- 컬러 이미지: RGB(Red, Green, Blue) 컬러 모델을 기반으로 이미지 저장
- 각 픽셀(pixel)은 RGB의 조합(8*3=24bit, 약 16.7백만 가지 색상)으로 표현됨
- 사진과 같은 화려한 색상과 유연한 그림에 적합
- 이미지 파일 포맷: JPEG, PNG, GIF, BMP, TIFF 등
- 컬러 이미지: RGB(Red, Green, Blue) 컬러 모델을 기반으로 이미지 저장
- 벡터(vector) 기법: 이미지의 특성을 명령어의 집합으로 표현하는 방식
- 수학적인 형태로 모델화되어 있어서 크기, 조절, 회전, 선의 굵기, 색상 등의 특성을 쉽게 변경시킬 수 있음
- 이미지를 확대하거나 축소해도 화질이 훼손되지 않음 (해상도 독립적)
- 예: TrueType(폰트), PostScript(그래픽)
소리 표현
- 소리 표현 원리: 일정 간격으로 소리 파동의 진폭 샘플을 추출하여 얻은 일련의 값을 인코딩함
연속적인 소리파동 → 샘플화 → 양자화 → 부호화
- 실제 오디오를 표현하는 샘플링 기법: 초당 샘플수 (samples/sec)
- 장거리 전화: 8,000 samples/sec
- CD 음악: 44,100 samples/sec
- CD 음악 초당 요구되는 비트수:
- 한 샘플을 16비트로 인코딩: 44,100 * 16 bits = 705,600 bits/sec = 88,200 바이트 필요
- 한 샘플을 32비트(스테레오의 경우)로 인코딩: 44,100 * 32 bits * 2 channels = 2,822,400 bits/sec = 352,800 바이트 필요
2진 체계
- 숫자의 값이 자릿수에 따라 위치 가중치를 가짐
- 표현: $a_n a_{n-1} \dots a_1 a_0 . a_{-1} a_{-2} \dots a_{-m}$
- 해석: $a_n,r^n + a_{n-1},r^{n-1} + \cdots + a_0,r^0 + a_{-1},r^{-1} + \cdots + a_{-m},r^{-m}$
- $a_i$는 위치 계수: 0 ~ r-1
- $r$은 기수(base): 예) 2, 10, 16
- $n$은 위치값 (정수부): 0, 1, 2, ...
- $-m$은 위치값 (소수부): -1, -2, ...
예시: $(1011)_r$
- r=2인 경우: 2진법(binary decimal notation)
- $(1011)_2 = 1\cdot2^3 + 0\cdot2^2 + 1\cdot2^1 + 1\cdot2^0$
- r=10인 경우: 10진법(ten decimal notation)
- $(1011)_{10} = 1\cdot10^3 + 0\cdot10^2 + 1\cdot10^1 + 1\cdot10^0$
- r=16인 경우: 16진법(hexa decimal notation)
- $(1011)_{16} = 1\cdot16^3 + 0\cdot16^2 + 1\cdot16^1 + 1\cdot16^0$
2진법 (binary number)
기수(base)가 2인 숫자 체계
- 2진수로 8비트에 저장할 수 있는 자연수의 범위: 0 ~ 255
- (00000000)₂ ~ (11111111)₂ → (0 ~ 255)$_{10}$
- 2진수로 n개 비트로 표현할 수 있는 자연수의 범위: $0\sim2^n - 1$
십진법 13의 2진법 표현을 구하는 알고리즘: (나눗셈 이용)
- 단계 1: 주어진 십진수 값을 2로 나누고 나머지를 기록한다.
- 단계 2: 단계 1의 몫이 0이 아니면, 이 몫을 2로 나누고 그 나머지를 기록하는 작업을 계속한다.
- 단계 3: 단계 1의 몫이 0이 되면, 나머지들을 기록된 순서대로 오른쪽에서 왼쪽으로 나열하면 십진 값의 2진법 표현을 얻는다.
- 13 / 2 = 6 ... 1
- 6 / 2 = 3 ... 0
- 3 / 2 = 1 ... 1
- 1 / 2 = 0 ... 1
- 결과: 1101₂
- 13 / 2 = 6 ... 1
16진법 (hexadecimal)
기수(base)가 16인 숫자 체계
- 긴 비트 열 (비트 스트림: stream)을 사람이 다루기 쉽지 않음
- 16진법은 4비트 패턴의 표시에 기호 하나를 사용하는 표기법
- 예) 0xB53
- (0~15)$_{10}$ 숫자를 2진수 4자리, 16진수 1자리로 표현 (0~9는 숫자, 10~15는 A~F)
2진수를 16진수로 표현하는 알고리즘
- 2진수 비트 열을 소수점 기준으로 4개씩 묶는다.
- 소수점 왼쪽(정수부): 오른쪽부터 4개씩 묶고, 마지막 묶음의 비트가 부족하면 왼쪽에 0을 채운다.
- 소수점 오른쪽(소수부): 왼쪽부터 4개씩 묶고, 마지막 묶음의 비트가 부족하면 오른쪽에 0을 채운다.
- 각 4비트 묶음을 해당하는 16진수 기호로 변환한다.
- 예: 10110001101011.1111001
- 정수부: 10 | 1100 | 0110 | 1011 → 2 | C | 6 | B
- 소수부: 1111 | 0010 (뒤에 0 세 개 채움) → F | 2
- 결과: 2C6B.F2$_{16}$
- 예: 10110001101011.1111001
2진 덧셈
2진수 덧셈 법칙:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 (올림수 1 발생)
- 전가산기(full adder): 2개의 입력 비트와 하나의 올림 비트를 입력 받아 합 비트와 올림 비트를 계산하는 회로
분수의 2진법 표현
- 2진수 101.101의 해석: 위치 가중치 이용
- $1\cdot2^2 + 0\cdot2^1 + 1\cdot2^0 + 1\cdot2^{-1} + 0\cdot2^{-2} + 1\cdot2^{-3}$
- $4 + 0 + 1 + \frac12 + 0 + \frac18 = 5\frac58$
정수의 저장
부호를 가진 정수(integer) 값을 비트 패턴으로 표현하는 방식
- 부호화 절대값(signed-magnitude) 표기법: 가장 왼쪽 비트는 부호 비트(0: 양수, 1: 음수), 나머지 비트는 절대값 표현
- 부호화된 (r-1)의 보수(signed (r-1)'s complement) 표기법
- 부호화된 r의 보수(signed r's complement) 표기법: 2의 보수(two's complement)가 대표적 (r=2)
- 초과(excess) 표기법 (excess notation)
정수를 저장하기 위한 기억장소 구조
- MSB(Most Significant Bit) 위치에 부호 비트 할당하고 나머지 비트에 데이터(값) 저장
- 양수: 부호 비트 0 | 음수: 부호 비트 1

r의 보수 표기법
- 정의: 정수 부분이 n 자릿수로 되어 있고 밑수가 r인 양수 N이 있을 때, N의 r의 보수는 r^n - N (N≠0일 때) 또는 0 (N=0일 때)로 정의됨
- (101100)₂ 2의 보수:
- 간편 계산법: 2진수에서 오른쪽부터 처음 1이 나올 때까지는 그대로 두고, 그 왼쪽 비트들은 모두 반전시킨다.
- (101100)₂ → 오른쪽 00 그대로 → 첫 1 그대로 → 왼쪽 101 반전 → 010
- 결과: 010100₂
- 또 다른 간편 계산법: 1의 보수를 구하고 1을 더한다. (1의 보수는 모든 비트 반전)
- (101100)₂ 의 1의 보수: (010011)₂
- 1의 보수 + 1: (010011)₂ + (1)₂ = (010100)
💡
2의 보수 표기법에서 1을 더하는 이유
1의 보수 체계에서는 +0
덕분에 자리 올림 이후에 추가적인 계산과정을 거칠 필요도 없고 오버플로 확인에도 용이해졌다.
1의 보수 체계에서는 +0
00000000 과 -0 11111111 이 서로 다른 비트 패턴으로 존재한다. 이는 효율이지 못하기에 2의 보수 체계에서는 0을 단 하나의 비트패턴 00000000 으로만 표현할 수 있도록 만들었다. 덕분에 -1 11111111 에 1을 더하면 자리 올림이 발생해 0 00000000이 되도록 구현해 한자리를 더 표현할 수 있다.덕분에 자리 올림 이후에 추가적인 계산과정을 거칠 필요도 없고 오버플로 확인에도 용이해졌다.
2의 보수에 의한 뺄셈 알고리즘 (M - N 계산):
- 1단계: 피감수 M에 감수 N의 2의 보수를 더한다. (M + (N의 2의 보수))
- 2단계: 위의 결과를 끝자리(가장 왼쪽 비트 넘어가는 올림수) 올림수에 관해 조사한다.
- (1) 끝자리 올림수가 있으면 올림수를 무시한다. (결과가 양수) (자체로 10진수)
- (2) 끝자리 올림수가 생기지 않았다면 단계 1에서 얻은 결과를 다시 2의 보수로 취하고 앞에 음의 부호를 붙인다. (결과가 음수) (10진수로 변환하는 과정을 거쳐야함!)
오버플로(overflow) 문제
- 정의: 주어진 비트 수에 저장할 수 있는 값의 범위 밖의 값을 저장하고자 시도할 때 발생하는 오류
- 발생 조건: 두 양수끼리 더했을 때 부호가 음수가 되거나, 두 음수끼리 더했을 때 부호가 양수가 되면 발생함. 즉, 불가능한 자리 올림이 발생했을 경우에 발생한다.
- n비트에서 2의 보수 표현으로 저장할 수 있는 정수 범위: $-2^{(n-1)} \sim 2^{(n-1)} - 1$
- 오버플로 예:
- 8비트 2의 보수 범위: -128 ~ 127
- (01000110)₂ + (01010000)₂ = (10010110)₂ → 양수(70) + 양수(80) = 음수(-106) → 오버플로
- (10111010)₂ + (10110000)₂ = (01101010)₂ → 음수(-70) + 음수(-80) = 양수(106) → 오버플로
- 8비트 2의 보수 범위: -128 ~ 127
초과(excess) 표기법
- 정의: 8421 코드에 x값 (초과 값)을 더한 값을 0으로 한 다음, 2진법으로 세어나갈 때 나타나는 순서대로 모든 비트 패턴을 나열하는 표기법
- 초과 값(x): $2^{(n-1)} - 1$ 또는 2$^{(n-1)}$ 등 다양하게 사용 가능
- 4비트에서 8초과 표기법: 초과 값 x=8 ($2^{(4-1)} = 2^3$)
- 비트 패턴 (표현 값) = 십진수 값 - 8
- 1111 (15): 15-8 = 7
- 1110 (14): 14-8 = 6
- ...
- 1000 (8): 8-8 = 0
- ...
- 0000 (0): 0-8 = -8
- 비트 패턴 (표현 값) = 십진수 값 - 8
- 특징: 가장 작은 비트 패턴(0000)이 가장 작은 수(-8)를 나타내고, 가장 큰 비트 패턴(1111)이 가장 큰 수(7)를 나타낸다. 부호화 절대값이나 2의 보수와 달리 비트 패턴의 크기 순서와 값의 크기 순서가 일치한다.
소수(fraction)의 표현
소수점 이하 값이 있는 숫자 표현
- 8비트 고정소수점(fixed-point) 표기법: 전체 비트 중 일부를 정수부, 나머지를 소수부로 미리 고정하여 나누는 방식
- 예) 8비트에서 4비트는 정수부, 4비트는 소수부 (가상 소수점)
- 10.11$_{10}$ 표현 시 (가상 소수점 위치에 따라)
- 정수부 4비트, 소수부 4비트: 정수부 10 (1010₂), 소수부 0.11 (0.11₂ = 0.5 + 0.25 = 0.75)
- 1010.1100 (나머지 비트는 0으로 채움)
- 정수부 4비트, 소수부 4비트: 정수부 10 (1010₂), 소수부 0.11 (0.11₂ = 0.5 + 0.25 = 0.75)
- 단점: 아주 큰 수나 아주 작은 수를 표현하기 위해 많은 비트가 필요함 (표현 범위가 좁음)
- 10.11$_{10}$ 표현 시 (가상 소수점 위치에 따라)
- 예) 8비트에서 4비트는 정수부, 4비트는 소수부 (가상 소수점)
부동소수점(floating-point) 표기법
- 지수 표기를 위해 초과(excess) 표기법 사용
- 8비트 구조 예: (부호 비트 1) (지수 3비트, 4초과 표기) (유효숫자/가수 4비트)
- 실수 0 저장: 모든 비트를 0으로 설정
- 실수 10.11 저장:
- 십진수 2.75를 이진수로 변환
- 2.75(십진수) → 10.11(이진수)
- 정규형(normalized form)으로 변환: 0.1011 x $2^2$ (소수점을 가장 왼쪽 1의 오른쪽으로 이동, 여기서는 왼쪽으로 두칸 갔으므로 지수는 +2)
- 부호: 양수 (0)
- 지수: +2, 4초과 표기법 (3비트) 사용 시 2+4=6 → 110₂
- 유효숫자(가수): 정규화된 형태 0.1011 에서 소수점 이하 부분 (1011)
- 8비트 표현 (부호 1, 지수 3, 가수 4) 예: 0 | 110 | 1011
- 지수 표현할때 유효숫자가 원본이 되기 위해 지수가 얼마나 필요한지를 생각해야함
- 부동소수점 읽기:
- 비트 패턴 분석 → 부호, 지수 (초과값 빼기), 가수 추출
- 지수와 가수를 이용하여 원래 값 계산 (가수에 소수점 붙이고 2^(지수) 곱함)
- 예: 01101011 ( 0 | 110 | 1011)
- 부호: 0 (양수)
- 지수: (110)₂ - 4 (초과값) = 6 - 4 = +2
- 소수(가수): 0.1011₂
- 저장된 값: 0.1011₂ x 2² = 10.11₂ = 2 + 0.5 + 0.25 = 2.75$_{10}$
- 정규형으로 변환하는 이유:
- 유한한 비트수에서 더 많은 값을 저장해서 최대 정밀도를 높일 수 있음
💡
방향 헷갈림 방지
‑ 숫자를 저장 할 때는 소수점을 왼쪽으로 옮긴 칸 수를 그대로 “+ 지수”로 적어둔다.(오른쪽이면 −지수).
‑ 나중에 값을 읽을 때는 그 지수만큼 2를 곱해서 소수점을 원래 자리로 돌려놓는다.
(예: 왼쪽으로 2칸 옮겼다면 지수 +2, 계산할 때는 2²를 곱해 소수점을 오른쪽으로 2칸 되돌림)
‑ 숫자를 저장 할 때는 소수점을 왼쪽으로 옮긴 칸 수를 그대로 “+ 지수”로 적어둔다.(오른쪽이면 −지수).
‑ 나중에 값을 읽을 때는 그 지수만큼 2를 곱해서 소수점을 원래 자리로 돌려놓는다.
(예: 왼쪽으로 2칸 옮겼다면 지수 +2, 계산할 때는 2²를 곱해 소수점을 오른쪽으로 2칸 되돌림)
통신 오류
데이터 전송/저장 중 비트 패턴이 변경되는 현상
- 오류 발생 시점:
- 컴퓨터 내부에서 장치들 간 데이터 전송 시
- 컴퓨터 저장장치에 저장되어 있는 동안
- 컴퓨터에서 외부 장치로 데이터 전송 시
- 원인: 노이즈, 전자파, 먼지 등 외부 요인
- 해결책: 오류의 탐지/정정을 제공할 수 있는 인코딩 기법 필요
패리티 비트(parity bit)
데이터에 추가적인 비트(패리티 비트)를 사용하여 오류를 탐지하는 방법
- 작동 원리
- 데이터의 비트 패턴 안의 1의 개수를 홀수(odd parity) 또는 짝수(even parity) 개가 되도록 패리티 비트를 조작하여 추가함
- 전송 후 1의 개수가 약속된 규칙(짝수/홀수)과 다르게 발견될 경우 오류 발생으로 판단함
홀수 패리티(odd parity) 인코딩 체계 예:
- ASCII A (01000001): 1의 개수 2개 (짝수) → 패리티 비트 1 추가 → 1 | 01000001 (전체 1의 개수 3개, 홀수)
- ASCII F (01000110): 1의 개수 3개 (홀수) → 패리티 비트 0 추가 → 0 | 01000110 (전체 1의 개수 3개, 홀수)
- 전송된 패턴의 1의 개수를 세어 홀수이면 오류 없음, 짝수이면 오류 발생으로 판단
패리티 비트 사용의 한계:
- 패리티 비트 패턴에서 짝수 개의 비트 오류가 발생하면 탐지하지 못함
- 예) 111000101 (pb=1, 홀수 패리티)
- 1비트 오류 (1→0): 101000101 (1의 개수 3개, 홀수) → 오류 검출 가능
- 2비트 오류 (1→0, 1→0): 110000001 (1의 개수 3개, 홀수) → 오류 검출 불가
- 3비트 오류 (1→0, 1→0, 0→1): 101100100 (1의 개수 4개, 짝수) → 오류 검출 가능
- 예) 111000101 (pb=1, 홀수 패리티)
CRC (Cyclic Redundancy Check)
- 전송되는 데이터에 특정 다항식을 나누어 나머지(CRC 값)를 생성하여 오류를 탐지
- 패리티 비트보다 신뢰도가 높으며 네트워크 통신 및 하드 디스크에서 널리 사용됨
체크섬 (Checksum)
- 데이터 블록의 모든 비트를 덧셈하여 합계를 기록하고, 수신 측에서 이를 비교하여 오류를 검출하는 방식
- 간단한 방식으로 네트워크 프로토콜(TCP/IP 등)에서 자주 사용됨
해밍 코드 (Hamming Code)
- 데이터 전송 과정에서 발생한 오류를 검출하고, 동시에 일부 오류를 자동으로 복구(정정)할 수 있는 방식
- 대표적으로 해밍(7,4) 코드가 있으며, 4비트의 데이터에 3비트의 정정용 비트를 추가하여 1비트 오류를 정정함
| 방식 | 특징 | 오류 검출 | 오류 정정 | 활용 예 |
|---|---|---|---|---|
| 패리티 비트 | 간단한 구현 | 가능(제한적) | 불가능 | RAM |
| CRC | 높은 신뢰성 | 가능(강력) | 불가능 | 네트워크, HDD |
| 체크섬 | 계산이 간편함 | 가능(중간) | 불가능 | TCP/IP |
| 해밍 코드 | 오류 정정 가능 | 가능 | 가능 | RAM, 통신 |
레퍼런스
“이 글은 『컴퓨터 과학 총론』(Brookshear & Brylow, 2019)의 내용을 토대로 재구성된 자료입니다.”
ƎXCLUSIVE ARCHITECTURE

Operating Systems: Mass-Storage Structure
💻 이 글은 컴퓨터시스템개론 시리즈의 일부입니다.



