스택

스택이란?

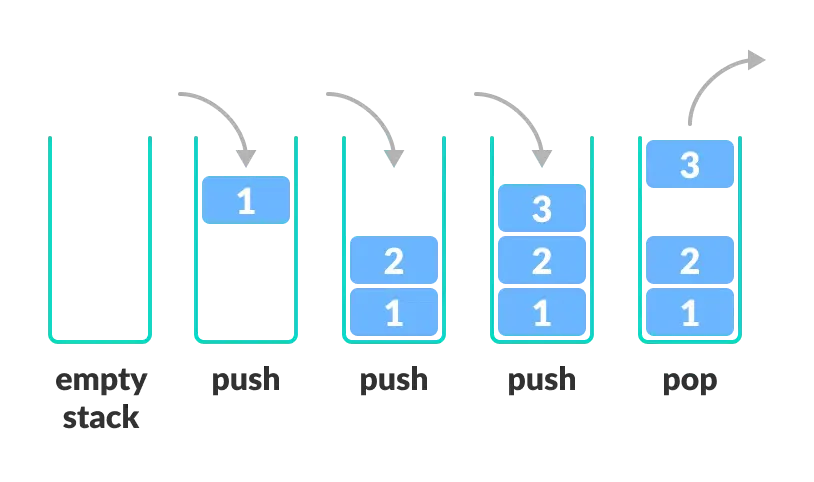
스택의 개념 및 특징

• 스택(stack): 문자 그대로 '쌓아놓은 더미'를 의미
  • ex) 쌓여 있는 접시 더미
• 후입선출(LIFO: Last-In First-Out) 원리: 가장 마지막(최근)에 들어온 데이터(접시)가 가장 먼저 나가는(꺼내지는) 구조
• 입출력이 한쪽 끝에서만 제한적으로 이루어지는 자료구조이다.

스택의 구조

• 스택 상단(top): 데이터의 삽입(insertion)과 삭제(deletion)가 이루어지는 스택의 유일한 입출력 통로 (열린 곳)
• 요소(element) 또는 항목(item): 스택에 저장되는 각각의 데이터 값
• 상태(State)
  • 공백 상태(empty): 스택에 아무 요소도 없는 상태
  • 포화 상태(full): 스택이 할당된 공간에 꽉 차서 더 이상 요소를 삽입할 수 없는 상태
• 주요 연산: 스택의 상태를 변화시키는 핵심 연산
  • 삽입(push): 스택의 top에 새로운 요소를 추가하는 연산
  • 삭제(pop): 스택의 top에서 요소를 제거하고 반환하는 연산

스택의 추상 자료형 (ADT)

스택 ADT 정의

• 데이터(Data): 후입선출(LIFO)의 접근 방식을 유지하는 요소들의 모음
  • init(): 스택을 초기화하여 공백 상태로 만든다.
  • push(e): 요소 e를 스택의 맨 위(top)에 추가한다 (삽입).
  • pop(): 스택의 맨 위(top)에 있는 요소를 꺼내(삭제하고) 반환한다.
  • peek(): 스택의 맨 위(top)에 있는 요소를 삭제하지 않고 확인만 하여 반환한다.
  • is_empty(): 스택이 비어 있으면 TRUE(참), 아니면 FALSE(거짓)를 반환한다.
  • is_full(): 스택이 가득 차 있으면 TRUE(참), 아니면 FALSE(거짓)를 반환한다.

스택 연산 상세

• push(e): 스택의 top 위치에 새로운 요소 e를 삽입한다. 스택의 상태가 변화한다.
• pop(): 스택의 top 위치의 요소를 삭제하고 그 값을 반환한다. 스택의 상태가 변화한다.
• peek(): 스택의 top 위치의 요소를 확인만 하고 값을 반환한다. 스택의 상태는 변하지 않는다.
  • 만약 peek() 연산이 지원되지 않으면, pop()으로 확인 후 다시 push()하여 원래 상태를 유지할 수 있다.
• is_empty(): 스택이 비어 있는지(요소가 없는지) 검사한다.
• is_full(): 스택이 꽉 차 있는지(더 이상 삽입할 공간이 없는지) 검사한다.

스택 오류 상황

• 스택 오버플로(Overflow): 스택이 포화 상태일 때 push() 연산을 시도하면 발생하는 오류. 더 이상 요소를 삽입할 수 없다.
• 스택 언더플로(Underflow): 스택이 공백 상태일 때 pop()이나 peek() 연산을 시도하면 발생하는 오류. 삭제하거나 참조할 요소가 없다.
• 안정적 사용: 오류를 방지하기 위해 push() 전에는 is_full()을, pop()이나 peek() 전에는 is_empty()를 검사하는 것이 좋다.

배열을 이용한 스택 구현

구현 구조

• 1차원 배열: 스택의 요소들을 저장하기 위한 고정 크기의 배열 ex) Element data[MAX_SIZE]; (Element는 스택 요소의 자료형, MAX_SIZE는 배열의 크기 즉, 스택의 최대 용량)
• 상단 표시 변수 top: 정수형 변수로, 스택의 가장 마지막(최근)에 삽입된 요소의 배열 인덱스를 저장한다.

top 변수와 상태 정의

• 초기화 (공백 상태): 스택이 비어있음을 나타내기 위해 top 변수를 -1로 초기화한다. init() { top = -1; }
• 공백 상태 검사: top이 -1이면 스택은 비어있다. is_empty() { return top == -1; }
• 포화 상태 검사: top이 배열의 마지막 인덱스(MAX_SIZE - 1)와 같으면 스택은 가득 찬 상태이다. is_full() { return top == MAX_SIZE - 1; }
• 요소 저장 순서: 배열의 0번 인덱스부터 요소가 차례대로 저장되며, data[0]이 가장 먼저 들어온 요소(스택의 가장 아래쪽), data[top]이 가장 마지막에 들어온 요소(스택의 상단)이다.

배열 기반 스택 연산 구현 (알고리즘)

• init(): 스택을 공백 상태로 초기화한다.
  • top ← -1
• is_empty(): 스택이 비었는지 검사한다.
  • return (top == -1)
• is_full(): 스택이 꽉 찼는지 검사한다.
  • return (top == MAX_SIZE - 1)
• push(e): 요소를 스택에 삽입한다.
  1. if is_full(): 스택이 포화 상태인지 검사한다.
     • then error "overflow": 포화 상태면 오버플로 오류 처리.
  2. else: 포화 상태가 아니면,
     • top ← top + 1 : top 인덱스를 1 증가시킨다.
     • data[top] ← e : 증가된 top 위치에 요소 e를 저장한다.
• pop(): 스택에서 요소를 삭제하고 반환한다.
  1. if is_empty(): 스택이 공백 상태인지 검사한다.
     • then error "underflow": 공백 상태면 언더플로 오류 처리.
  2. else: 공백 상태가 아니면
     • e ← data[top] : 현재 top 위치의 요소를 임시 변수 e에 저장한다.
     • top ← top - 1 : top 인덱스를 1 감소시켜 요소를 논리적으로 삭제한다.
     • return e : 저장해 둔 요소 e를 반환한다.
• peek(): 스택 상단 요소를 확인만 한다.
  1. if is_empty(): 스택이 공백 상태인지 검사한다.
     • then error "underflow": 공백 상태면 언더플로 오류 처리.
  2. else: 공백 상태가 아니면
     • return data[top] : 현재 top 위치의 요소를 반환한다 (top 값은 변경하지 않음).

순차 자료구조 구현의 장단점

• 장점:
  • 순차 자료 구조인 1차원 배열을 사용하여 구현이 비교적 간단하고 쉽다.
• 단점:
  • 배열의 크기가 고정되어 있어 스택의 크기를 동적으로 변경하기 어렵다. (크기 예측 실패 시 문제 발생)
  • 배열 중간에 요소 삽입/삭제가 비효율적인 순차 자료구조의 단점을 그대로 가진다 (스택 연산은 top에서만 일어나므로 이 단점은 크게 부각되지 않음).

스택의 응용

스택은 입력 순서와 반대로 처리해야 하는 작업에 유용하게 사용된다.

시스템 스택 (함수 호출 관리)

• 운영체제는 프로그램 내 함수의 호출과 복귀 순서를 관리하기 위해 시스템 스택을 사용한다.
• 함수가 호출될 때마다 해당 함수 실행에 필요한 정보들을 스택 프레임(Stack Frame) 또는 활성화 레코드(Activation Record)라는 단위로 묶어 시스템 스택에 push한다.
  • 스택 프레임 포함 정보: 함수 내 지역 변수, 함수로 전달된 매개변수, 함수 실행 완료 후 돌아갈 복귀 주소 등
• 함수 실행이 끝나면, 해당 함수의 스택 프레임을 시스템 스택에서 pop하여 제거하고, 프레임에 저장된 복귀 주소로 돌아가 실행을 계속한다.
• 가장 마지막에 호출된 함수가 가장 먼저 실행을 완료하고 복귀하는 LIFO 구조이므로 스택이 효율적이다.

문자열 뒤집기 (역순 출력)

• 스택의 LIFO 특성을 활용하여 문자열을 쉽게 뒤집을 수 있다.
• 과정:
  1. 입력 문자열의 문자들을 앞에서부터 순서대로 스택에 push한다.
  2. 문자열 끝까지 삽입 후, 스택이 is_empty() 상태가 될 때까지 pop 연산을 반복한다.
  3. pop 되어 나오는 문자들을 순서대로 출력하면 원본 문자열의 역순이 된다.
• ex) “Oiiai” → 스택: [O, i, i, a, i] (i가 top) → pop 순서: i, a, i, i, O → 출력: “iaiiO”

괄호 검사

• 소스 코드, 수식 등에서 사용된 괄호 ( ), { }, [ ]의 쌍이 올바르게 사용되었는지 검사한다.
• 올바른 괄호 사용 조건:
  1. 개수: 왼쪽 괄호와 오른쪽 괄호의 개수가 같아야 한다.
  2. 짝: 같은 종류의 괄호끼리 쌍을 이루어야 하며, 왼쪽 괄호가 오른쪽 괄호보다 먼저 나와야 한다.
  3. 포함 관계: 괄호 사이에는 포함 관계만 존재해야 하며, 서로 다른 종류의 괄호가 교차하여 쌍을 이루면 안됨 ex) ( { } )는 OK, ( { ) }는 오류.
• 스택을 이용한 검사 알고리즘:
  1. 입력 문자열(수식)을 처음부터 끝까지 한 문자씩 읽는다.
  2. 왼쪽 괄호 ((, {, [)를 만나면 스택에 push한다.
  3. 오른쪽 괄호 (), }, ])를 만나면:
     • 스택이 is_empty()인지 확인한다. 비어있으면 짝이 맞는 왼쪽 괄호가 없는 것이므로 오류 (조건 2 위배)
     • 스택이 비어있지 않으면, pop 연산으로 스택 top의 괄호를 꺼낸다.
     • 꺼낸 왼쪽 괄호와 현재 만난 오른쪽 괄호가 짝이 맞는지 비교한다. 짝이 맞지 않으면 오류 (조건 3 위배)
  4. 괄호가 아닌 다른 문자는 무시한다.
  5. 입력 문자열을 끝까지 다 읽었을 때:
     • 스택이 is_empty() 상태이면 모든 괄호 쌍이 올바르게 사용된 것이므로 검사 성공
     • 스택에 왼쪽 괄호가 남아있으면 짝이 맞는 오른쪽 괄호가 부족한 것이므로 오류 (조건 1 위배)

계산기 프로그램 (수식 계산)

• 컴퓨터는 사람이 사용하는 중위 표기법(infix notation) 수식을 직접 계산하기 어렵다 (괄호, 연산자 우선순위 처리 복잡).
• 수식 표현법

• 컴퓨터의 계산 방식: 스택을 이용하여 중위 표기식을 후위 표기식으로 변환한 뒤, 후위 표기식을 계산한다.
  • 중위 표기 → 후위 표기 변환 → 후위 표기식 계산
• 후위 표기법의 장점:
  • 괄호가 필요 없다.
  • 연산자 우선순위를 고려할 필요가 없다. (식 자체에 순서가 내포됨)
  • 수식을 왼쪽에서 오른쪽으로 읽으면서 바로 계산이 가능하다.
• 후위 표기 수식 계산 알고리즘 (스택 활용):
  1. 피연산자를 저장할 스택을 준비한다.
  2. 후위 표기식을 왼쪽에서 오른쪽으로 스캔한다.
  3. 피연산자를 만나면 스택에 push한다.
  4. 연산자를 만나면 스택에서 피연산자 두 개를 pop한다. (주의: 먼저 pop된 것이 두 번째 피연산자, 나중에 pop된 것이 첫 번째 피연산자)
  5. 두 피연산자로 해당 연산을 수행하고, 그 결과를 다시 스택에 push한다.
  6. 수식 끝까지 처리하면 스택에는 최종 계산 결과 하나만 남게 된다. 이 값을 pop하여 반환한다.
• ex) 8 2 / 3 - 3 2 * + 계산
  • 8, 2 push → 스택: [8, 2]
  • / 만나면 2, 8 pop → 8/2=4 계산 → 4 push → 스택: [4]
  • 3 push → 스택: [4, 3]
  • - 만나면 3, 4 pop → 4-3=1 계산 → 1 push → 스택: [1]
  • 3, 2 push → 스택: [1, 3, 2]
  • * 만나면 2, 3 pop → 3*2=6 계산 → 6 push → 스택: [1, 6]
  • + 만나면 6, 1 pop → 1+6=7 계산 → 7 push → 스택: [7]
  • 최종 결과: 7
• 중위 표기 → 후위 표기 변환 알고리즘 (스택 활용):
  1. 연산자를 임시 저장할 스택을 준비한다.
  2. 중위 표기식을 왼쪽에서 오른쪽으로 스캔한다.
  3. 피연산자를 만나면 즉시 출력한다.
  4. 연산자를 만나면:
     • 스택이 비어있거나, 스택 top의 연산자가 '(' 이거나, 현재 연산자의 우선순위가 스택 top 연산자의 우선순위보다 높으면 현재 연산자를 스택에 push한다.
     • 그렇지 않으면 (현재 연산자 우선순위가 스택 top 연산자보다 낮거나 같으면), 스택 top 연산자의 우선순위가 현재 연산자보다 낮아질 때까지 스택에서 연산자를 pop하여 출력한 후, 현재 연산자를 스택에 push한다. (우선순위가 같은 경우도 pop함: 왼쪽 결합성 고려)
  5. 왼쪽 괄호 ( 를 만나면 무조건 스택에 push한다. (스택 내에서는 우선순위가 가장 낮게 취급)
  6. 오른쪽 괄호 ) 를 만나면 스택에서 (가 나올 때까지 연산자를 pop하여 출력한다. (는 출력하지 않고 버린다.
  7. 입력 수식을 끝까지 처리한 후, 스택에 남아 있는 모든 연산자를 pop하여 출력한다.
• 연산자 우선순위 예: *, / (높음=2) > +, - (중간=1) > ( (스택 내에서 낮음=0)

시스템 스택과 순환 호출

순환(Recursion)이란?

• 어떤 함수가 문제를 해결하기 위해 자기 자신을 다시 호출하는 프로그래밍 기법
• 적합한 경우:
  • 문제 자체가 순환적으로 정의되는 경우 (ex: 팩토리얼, 피보나치 수열)
  • 순환적으로 정의되는 자료구조를 다루는 경우 (ex: 트리 순회, 그래프 탐색)
• 구성 요소:
  • 순환 호출 부분: 문제의 크기를 줄여 자기 자신을 다시 호출하는 부분.
  • 순환 중단 부분 (Base Case): 더 이상 순환 호출을 하지 않고 결과를 바로 반환하는 부분. 문제의 크기가 충분히 작아졌을 때 해당한다.
• 주의: 순환 중단 부분이 없거나 도달할 수 없는 조건을 가지면 함수가 무한히 호출되어 시스템 스택 오버플로(Stack Overflow) 오류를 발생시킨다. 시스템 스택 공간이 모두 소진되기 때문이다.

순환 vs 반복(Iteration)

• 상호 변환: 많은 경우 순환 알고리즘은 반복문(for, while)을 사용하는 반복 알고리즘으로, 또는 그 반대로 변환할 수 있다.
• 실행 속도: 일반적으로 반복이 순환보다 빠르다. 순환은 함수 호출/복귀에 따른 오버헤드(스택 프레임 생성/제거 등)가 발생하기 때문이다.
• 코드 가독성/간결성: 특정 문제(특히 트리 관련)에 대해서는 순환 코드가 문제의 구조를 더 자연스럽게 반영하여 훨씬 명확하고 간결하게 작성될 수 있다. 반복으로 구현하면 코드가 복잡해질 수 있다.
• 메모리 사용: 순환은 호출 깊이만큼 시스템 스택 메모리를 사용한다. 깊이가 너무 깊어지면 스택 오버플로 위험이 있다. 반복은 스택 사용량이 상대적으로 적다.

분할 정복(Divide and Conquer)

• 순환은 복잡한 문제를 해결하기 위해 문제를 더 작은 크기의 동일한(또는 유사한) 부분 문제들로 나누고(Divide), 각 부분 문제를 해결한 후(Conquer), 그 결과들을 결합하여 원래 문제의 답을 얻는 분할 정복 설계 전략을 자연스럽게 구현하는 경우가 많다.

순환의 예: 팩토리얼(Factorial)

• 정의: n! = n * (n-1) * (n-2) * ... * 1 (단, 0! = 1)
• 순환적 정의:
  • n! = 1 (if n = 0 or n = 1) <-- 중단 부분 (Base Case)
  • n! = n * (n-1)! (if n > 1) <-- 순환 호출 부분

구현 예:

int factorial(int n) {
    if (n <= 1) { // 중단 부분
        return 1;
    } else { // 순환 호출 부분
        return n * factorial(n - 1);
    }
}

순환의 예: 하노이의 탑(Tower of Hanoi)

• 문제: 세 개의 막대(A, B, C)가 있고, 첫 번째 막대(A)에 크기가 다른 n개의 원판이 크기 순서대로 쌓여있다. 이 원판들을 다른 막대(C)로 모두 옮기는 문제
• 규칙:
  1. 한 번에 하나의 원판만 옮길 수 있다.
  2. 맨 위에 있는 원판만 옮길 수 있다.
  3. 크기가 작은 원판 위에 큰 원판을 쌓을 수 없다.
  4. 중간 막대(B)를 임시로 사용할 수 있다.
• 순환적 해결 과정: hanoi_tower(n, from, tmp, to) - n개의 원판을 from 막대에서 to 막대로 tmp 막대를 이용하여 옮기는 함수
  1. [n-1개 옮기기] hanoi_tower(n-1, from, to, tmp): from 막대에 있는 위의 n-1개 원판을 tmp 막대로 옮긴다 (to 막대를 임시로 사용).
  2. [가장 큰 원판 옮기기] from 막대에 남은 가장 큰 원판(n번째)을 to 막대로 옮긴다. (이동 과정 출력)
  3. [n-1개 다시 옮기기] hanoi_tower(n-1, tmp, from, to): tmp 막대에 있는 n-1개 원판을 to 막대로 옮긴다 (from 막대를 임시로 사용).
  4. 중단 부분 (Base Case): 옮겨야 할 원판의 개수 n이 1일 때. 해당 원판을 from에서 to로 바로 옮기고 종료한다.

구현 예:

void hanoi_tower(int n, char from, char tmp, char to) {
    if (n == 1) { // 중단 부분
        printf("원판 1: %c -> %c\n", from, to);
    } else { // 순환 호출 부분
        hanoi_tower(n - 1, from, to, tmp); // 1단계
        printf("원판 %d: %c -> %c\n", n, from, to); // 2단계
        hanoi_tower(n - 1, tmp, from, to); // 3단계
    }
}

레퍼런스

“이 글은 『쉽게 배우는 C 자료구조』(최영규 및 천인국, 2024)의 내용을 토대로 재구성된 자료입니다.”​